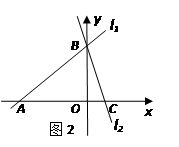题目内容
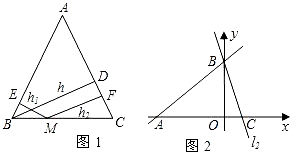
运用“同一图形的面积不同表示方式相同”可以证明一类含有线段的等式,这种解决问题的方法我们称之为面积法.(1)如图1,在等腰三角形ABC中,AB=AC,AC边上的高为h,M是底边BC上的任意一点,点M到腰AB、AC的距离分别为h1、h2.请用面积法证明:h1+h2=h;
(2)当点M在BC延长线上时,h1、h2、h之间的等量关系式是
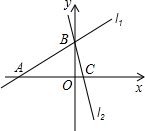
(3)如图2在平面直角坐标系中有两条直线l1:y=
| 3 | 4 |
分析:(1)连接AM,△ABC被分成△ABM和△ACM两个三角形,根据三角形的面积公式底乘以高除以2分别求解,再根据S△ABC=S△ABM+S△AMC整理即可得到h1+h2=h.
(2)根据(1)的方法,利用三角形面积的关系求解即可;
(3)先根据直线关系式求出A、B、C三点的坐标利用勾股定理求出AB=AC,所以△ABC是等腰三角形,再分点M在线段BC上和CB的延长线上两种情况讨论求解.
(2)根据(1)的方法,利用三角形面积的关系求解即可;
(3)先根据直线关系式求出A、B、C三点的坐标利用勾股定理求出AB=AC,所以△ABC是等腰三角形,再分点M在线段BC上和CB的延长线上两种情况讨论求解.
解答:解:(1)∵S△ABC=S△ABM+S△AMC,S△ABM=
×AB×ME=
×AB×h1,S△AMC=
×AC×MF=
×AC×h2,
又∵S△ABC=
×AC×BD=
×AC×h,
∴
×AC×h=
×AB×h1+
×AC×h2,
∴h1+h2=h.
(2)h1-h2=h.
(3)在y=
x+3中,令x=0得y=3;令y=0得x=-4,则:
A(-4,0),B(0,3)同理求得C(1,0),
AB=
=5,AC=5,
所以AB=AC,即△ABC为等腰三角形.
①当点M在BC边上时,由h1+h2=h得:
1+My=OB,My=3-1=2,把它代入y=-3x+3中求得:Mx=
,
∴M(
,2);
②当点M在CB延长线上时,由h1-h2=h得:My-1=OB,My=3+1=4,
把它代入y=-3x+3中求得:Mx=-
,
∴M(-
,4),
∴点M的坐标为(
,2)或(-
,4).
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴h1+h2=h.
(2)h1-h2=h.
(3)在y=
| 3 |
| 4 |
A(-4,0),B(0,3)同理求得C(1,0),
AB=
| OA2+OB2 |
所以AB=AC,即△ABC为等腰三角形.
①当点M在BC边上时,由h1+h2=h得:
1+My=OB,My=3-1=2,把它代入y=-3x+3中求得:Mx=
| 1 |
| 3 |
∴M(
| 1 |
| 3 |
②当点M在CB延长线上时,由h1-h2=h得:My-1=OB,My=3+1=4,
把它代入y=-3x+3中求得:Mx=-
| 1 |
| 3 |
∴M(-
| 1 |
| 3 |
∴点M的坐标为(
| 1 |
| 3 |
| 1 |
| 3 |
点评:解答本题的关键在于利用等腰三角形两边相等的性质和三角形面积的关系,利用面积求解在几何解答题中经常用到,同学们在答题时一定要灵活运用.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目



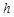 ,M是底边BC上的任意一点,点M到腰AB、AC的距离分别为
,M是底边BC上的任意一点,点M到腰AB、AC的距离分别为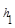 、
、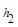 .连接AM,可得结论
.连接AM,可得结论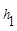 +
+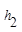 =
=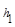 、
、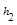 、
、
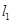 :
: 、
、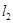 :
: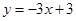 ,若
,若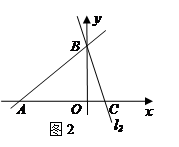
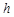 ,M是底边BC上的任意一点,点M到腰AB、AC的距离分别为
,M是底边BC上的任意一点,点M到腰AB、AC的距离分别为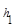 、
、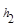 .连接AM,可得结论
.连接AM,可得结论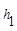 +
+ =
= 、
、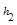 、
、
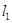 :
: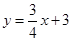 、
、 :
: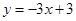 ,若
,若