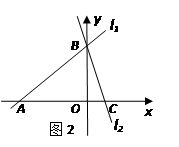题目内容
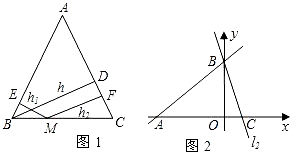
运用“同一图形的面积不同表示方式相同”可以证明一类含有线段的等式,这种解决问题的方法我们称之为面积法.【小题1】如图1,在等腰三角形ABC中,AB=AC,AC边上的高为
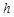 ,M是底边BC上的任意一点,点M到腰AB、AC的距离分别为
,M是底边BC上的任意一点,点M到腰AB、AC的距离分别为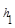 、
、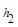 .连接AM,可得结论
.连接AM,可得结论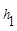 +
+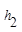 =
=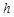 .当点M在BC延长线上时,
.当点M在BC延长线上时,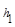 、
、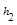 、
、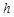 之间的等量关系式是 .(直接写出结论不必证明).
之间的等量关系式是 .(直接写出结论不必证明).
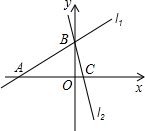
【小题2】应用:平面直角坐标系中有两条直线
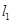 :
: 、
、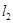 :
: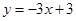 ,若
,若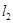 上的一点M到
上的一点M到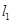 的距离是1.请运用(1)的条件和结论求出点M的坐标.
的距离是1.请运用(1)的条件和结论求出点M的坐标.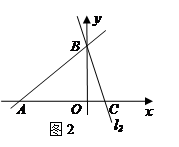
【小题1】)
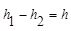 .
. 【小题2】在
 中,令
中,令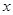 =0得
=0得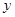 = 3;令
= 3;令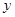 = 0得
= 0得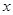 =-4 ,则:
=-4 ,则:A(-4,0),B(0,3)同理求得C(1,0).
AB=
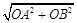 =" 5 " AC="5 "
=" 5 " AC="5 " 所以AB=AC,即△ABC为等腰三角形.
① 当点M在BC边上时,由
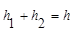 得:
得:1+
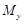 =OC.
=OC.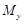 =3-1=2,把它代入
=3-1=2,把它代入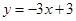 中求得:
中求得: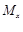 =8,
=8,∴M(
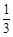 ,2);
,2);②当点M在CB延长线上时,由
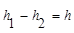 得:
得: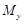 -1="OC."
-1="OC." 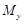 =3+1=4,把它代入
=3+1=4,把它代入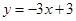 中求得:
中求得: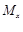 =
= 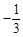 ,
,∴M(
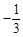 ,4).
,4). ∴点M的坐标为(
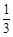 ,2)或(
,2)或(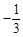 ,4).解析:
,4).解析:略

练习册系列答案
相关题目



 ,M是底边BC上的任意一点,点M到腰AB、AC的距离分别为
,M是底边BC上的任意一点,点M到腰AB、AC的距离分别为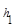 、
、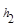 .连接AM,可得结论
.连接AM,可得结论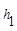 +
+ =
= 、
、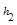 、
、
 :
: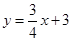 、
、 :
: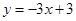 ,若
,若