题目内容
 如图所示,某小区有一块长为32米,宽为15米的矩形草坪,现要在草坪中间设计一横二竖的等宽的小路供居民散步,要使草地的面积是整个矩形草坪总面积的
如图所示,某小区有一块长为32米,宽为15米的矩形草坪,现要在草坪中间设计一横二竖的等宽的小路供居民散步,要使草地的面积是整个矩形草坪总面积的| 7 | 8 |
分析:把小路均平移到矩形的一边,可得草地的面积为边长为32-2x,15-x的矩形,等量关系为:边长为32-2x,15-x的矩形草地的面积=
×原矩形草地的面积.
| 7 |
| 8 |
解答:解:平移后可得草地的面积为边长为32-2x,15-x的矩形,
∴可得方程为(32-2x)(15-x)=
×32×15,
故答案为(32-2x)(15-x)=
×32×15.
∴可得方程为(32-2x)(15-x)=
| 7 |
| 8 |
故答案为(32-2x)(15-x)=
| 7 |
| 8 |
点评:考查列一元二次方程;把小路进行平移得到平移后草地矩形的长与宽是解决本题的突破点.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
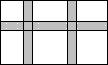 如图所示,某小区有一块长为32米,宽为15米的矩形草坪,现要在草坪中间设计一横二竖的等宽的小路供居民散步,要使小路的面积是草地总面积的八分之一,求小路的宽是
如图所示,某小区有一块长为32米,宽为15米的矩形草坪,现要在草坪中间设计一横二竖的等宽的小路供居民散步,要使小路的面积是草地总面积的八分之一,求小路的宽是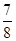 ,若设小路
,若设小路
 ,若设小路的宽为是x米,那么所得的方程是 .
,若设小路的宽为是x米,那么所得的方程是 .
