题目内容
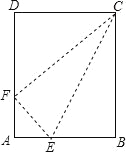
【题目】如图将一张矩形纸片ABCD沿CE折叠,使得B点恰好落在AD边上,设此点为F,若AB:BC=4:5,则tan∠ECF的值是_____;
【答案】![]()
【解析】
根据已知条件设AB=4k,则BC=5k;先求出DF的长(用k表示),再求出AF的长;借助勾股定理求出BE的长,进而根据三角函数求出tan∠ECF的值,即可解决问题.
解:
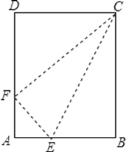
∵AB:BC=4:5,
∴设AB=4k,则BC=5k;
∵四边形ABCD为矩形,
∴∠A=∠B=∠D=90°;
DC=AB=4k,AD=BC=5k;
由题意得:CF=BC=5k,BE=EF(设为m),
则AE=4k﹣m;由勾股定理得:
DF2=CF2﹣CD2=25k2﹣16k2,
∴DF=3k,AF=5k﹣3k=2k;
由勾股定理得:m2=(4k﹣m)2+(2k)2,
解得:m=![]() k;
k;
tan∠ECF=tan∠ECB=![]() =
=![]() .
.
故答案为:![]() .
.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目