题目内容
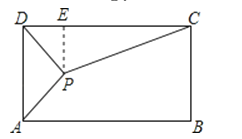
【题目】如图,矩形ABCD中,AB=2AD,AP平分∠DAB,且AP⊥DP于点P,连接CP,则sin∠DCP的值是 .
【答案】![]()
【解析】解:过点P作PE⊥CD于点E,
∵四边形ABCD是矩形,
∴CD=AB,∠DAB=∠ADC=90°.
∵AP是∠DAB的角平分线,
∴∠DAP=![]() ∠DAB=45°.
∠DAB=45°.
∵DP⊥AP,
∴∠APD=90°.
∴∠ADP=45°.
∴∠CDP=45°.
在Rt△APD中,DP=![]() AD,
AD,
在Rt△DEP中,∠DEP=90°,
∴PE=![]() PD=
PD=![]() AD,
AD,
∴CE=CD﹣DE,
∵AB=2AD,
∴CE=CD﹣DE=2AD﹣![]() AD=
AD=![]() AD
AD
在Rt△DEP中,∠CEP=90°,PC=![]() =
=![]() AD,
AD,
∴sin∠DCP=![]() =
=![]() =
=![]() .
.
所以答案是:![]() .
. 
【考点精析】解答此题的关键在于理解矩形的判定方法的相关知识,掌握有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目