题目内容
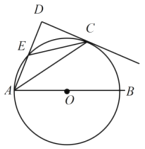
【题目】如图,点O在ABCD的AD边上,⊙O经过A、B、C三点,点E在⊙O外,且OE⊥BC,垂足为F.
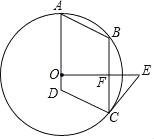
(1)若EC是⊙O的切线,∠A=65°,求∠ECB的度数;
(2)若OF=4,OD=1,求AB的长.
【答案】(1)40°;(2)2![]()
【解析】
(1)连接OB、OC,如图,利用平行四边形的性质和等腰三角形的性质计算出∠OCB=50°,即可得到结论;
(2)作DH⊥BC于H,如图,设⊙O的半径为r,则AD=r+1,利用平行四边形的性质得BC=AD=r+1,AD∥BC,AB=CD,再根据垂径定理得BF=CF=![]() (r+1),在Rt△OCF中利用勾股定理得到42+
(r+1),在Rt△OCF中利用勾股定理得到42+![]() (r+1)2=r2,解方程得到r=5,然后在Rt△CDH中利用勾股定理计算CD即可得到AB的长.
(r+1)2=r2,解方程得到r=5,然后在Rt△CDH中利用勾股定理计算CD即可得到AB的长.
解:(1)连接OB、OC,如图,
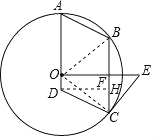
∵EC是⊙O的切线,
∴∠OCE=90°,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠ABC=180°﹣∠A=180°﹣65°=115°,
∵OA=OB,
∴∠OBA=∠A=65°,
∴∠OBC=115°﹣65°=50°,
∴∠OCB=50°,
∴∠BCE=∠OCE﹣∠OCB=90°﹣50°=40°;
(2)解:作DH⊥BC于H,如图,设⊙O的半径为r,则AD=r+1,
∵四边形ABCD为平行四边形,
∴BC=AD=r+1,AD∥BC,AB=CD,
∵OE⊥BC,
∴四边形ODHF为矩形,BF=CF=![]() (r+1),
(r+1),
∴FH=OD=1,DH=OF=4,
在Rt△OCF中,42+![]() (r+1)2=r2,解得r1=﹣
(r+1)2=r2,解得r1=﹣![]() (舍去),r2=5,
(舍去),r2=5,
在Rt△CDH中,∵CH=2,DH=4,
∴CD=![]() =2
=2![]() ,
,
∴AB=2![]() .
.

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案【题目】已知一次函数y1=kx+m(k≠0)和二次函数y2=ax2+bx+c(a≠0)的自变最x和对应函数值y1,y2的部分对应值如表:
x | … | ﹣1 | 0 | 2 | 4 | … |
y1 | … | 0 | 1 | 3 | 5 | … |
x | … | ﹣1 | 1 | 3 | 4 | … |
y2 | … | 0 | ﹣4 | 0 | 5 | … |
当y1≥y2时,自变量x的取值范图是_____.