��Ŀ����
����Ŀ�����κ���y=ax2+bx+4��ͼ����x�ύ������A��B����y�ύ�ڵ�C����A����1��0����B��4��0��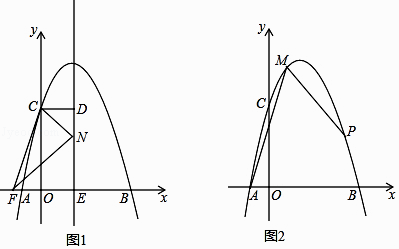
��1����˶��κ����ı���ʽ
��2����ͼ1�������ߵĶԳ���m��x�ύ�ڵ�E��CD��m������ΪD����F���� ![]() ��0��������N���߶�DE���˶�������CF��CN��FN�����Ե�C��D��NΪ��������������FEN���ƣ����N������
��0��������N���߶�DE���˶�������CF��CN��FN�����Ե�C��D��NΪ��������������FEN���ƣ����N������
��3����ͼ2����M���������ϣ��ҵ�M�ĺ�������1����PΪ��������һ���㣬����PMA=45�㣬���P�����꣮
���𰸡�
��1��
�⣺��x=0ʱ��y=4��
��C��0��4����
�������ߵĽ���ʽΪy=a��x+1����x��4��������C���������ã���4a=4�����a=��1��
�������ߵĽ���ʽΪy=��x2+3x+4
��2��
�⣺x=�� ![]() =
= ![]() ��
��
��CD= ![]() ��EF=
��EF= ![]() ��
��
���N�������� ![]() ��a����ND=4��a��NE=a��
��a����ND=4��a��NE=a��
����CDN�ס�FENʱ�� ![]() ����
���� ![]() �����a=
�����a= ![]() ��
��
���N�������� ![]() ��
�� ![]() ����
����
����CDN�ס�NEFʱ�� ![]() ����
���� ![]() =
= ![]() ����ã�a=2��
����ã�a=2��
���N�������� ![]() ��2����
��2����
������������N�������� ![]() ��
�� ![]() ����
���� ![]() ��2��
��2��
��3��
�⣺��ͼ��ʾ������A��AD��y�ᣬ����M��DM��x�ᣬ����ΪD������A��AE��AM��ȡAE=AM����EF��x�ᣬ����ΪF������EM�����������P��

��AM=AE����MAE=90�㣬
���AMP=45�㣮
��x=1���������ߵĽ���ʽ�ã�y=6��
���M��������1��6����
��MD=2��AD=6��
�ߡ�DAM+��MAF=90�㣬��MAF+��FAE=90�㣬
���DAM=��FAE��
�ڡ�ADM�͡�AFE�У�  ��
��
���ADM�ա�AFE��
��EF=DM=2��AF=AD=6��
��E��5����2����
��EM�Ľ���ʽΪy=kx+b��
����M�͵�E���������ã� ![]() �����k=��2��b=8��
�����k=��2��b=8��
��ֱ��EM�Ľ���ʽΪy=��2x+8��
��y=��2x+8��y=��x2+3x+4��������ã�x=1��x=4��
��x=4����y=��2x+8�ã�y=0��
���P��������4��0��
����������1������õ�C�����꣬�������ߵĽ���ʽΪy=a��x+1����x��4��������C������������a��ֵ���Ӷ��õ������ߵĽ���ʽ����2������������ߵĶԳ��ᣬȻ�����CD��EF�ij������N������Ϊ��0��a����ND=4��a��NE=a��Ȼ���������������ε������г�����a�ķ��̣�Ȼ������a��ֵ����3������A��AD��y�ᣬ����M��DM��x�ᣬ����ΪD������A��AE��AM��ȡAE=AM����EF��x�ᣬ����ΪF������EM�����������P�����AMEΪ����ֱ�������Σ�Ȼ������õ�M�����꣬�Ӷ��ɵõ�MD=2��AD=6��Ȼ��֤�����ADM�ա�AFE�����ǿɵõ���E�����꣬Ȼ�����EM�Ľ���ʽΪy=��2x+8��������ֱ��EM�������ߵĽ������꼴�ɣ�

 ������ϵ�д�
������ϵ�д�����Ŀ��ij��ѧ������У�����������ִ������������в����ݳ����ɼ�����ѡ��![]() ��ѡ����ɳ��д����Ӻ��д����Ӳμ�ѧУ������ÿ����
��ѡ����ɳ��д����Ӻ��д����Ӳμ�ѧУ������ÿ����![]() ��ѡ�ֵľ����ɼ���ͼ��ʾ��
��ѡ�ֵľ����ɼ���ͼ��ʾ��

![]() �����
�����
ƽ�������֣� | ��λ�����֣� | �������֣� | |
������� |
|
| |
������� |
|
|
![]() ������Ӿ����ɼ���ƽ��������λ���������ĸ������ӵijɼ��Ϻã�
������Ӿ����ɼ���ƽ��������λ���������ĸ������ӵijɼ��Ϻã�
![]() �������Ӿ����ɼ��ķ�����ж��ĸ������ӵijɼ���Ϊ�ȶ���
�������Ӿ����ɼ��ķ�����ж��ĸ������ӵijɼ���Ϊ�ȶ���