题目内容
若a、b、c、d是乘积为1的4个正数，则代数式a2+b2+c2+d2+ab+ac+ad+bc+bd+cd的最小值为
- A.0
- B.4
- C.8
- D.10
D
分析：将abcd=1变形得cd=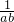
，得出ab+cd=ab+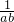≥2，同理得出a2+b2+c2+d2≥2ab+2cd≥4，进而解决．
解答：由abcd=1，得cd=，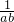
则ab+cd=ab+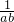≥2，
同理ac+bd≥2，ad+bc≥2，
又a2+b2+c2+d2≥2ab+2cd=2（ab+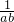）≥4，
故a2+b2+c2+d2+ab+ac+ad+bc+bd+cd≥10．
故选D．
点评：此题主要考查了数的乘积的一种等量代换，得出ab+cd=ab+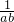≥2，是解决问题的关键．
分析：将abcd=1变形得cd=
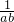，得出ab+cd=ab+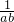≥2，同理得出a2+b2+c2+d2≥2ab+2cd≥4，进而解决．解答：由abcd=1，得cd=
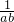，则ab+cd=ab+
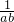≥2，同理ac+bd≥2，ad+bc≥2，
又a2+b2+c2+d2≥2ab+2cd=2（ab+
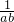）≥4，故a2+b2+c2+d2+ab+ac+ad+bc+bd+cd≥10．
故选D．
点评：此题主要考查了数的乘积的一种等量代换，得出ab+cd=ab+
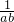≥2，是解决问题的关键． 
练习册系列答案
名校课堂系列答案
相关题目