题目内容
【题目】平面直角坐标系中，点P的坐标为（m，n），则向量
可以用点P的坐标表示为=（m，n）；已知
=（x1，y1），
=（x2，y2），若x1x2+y1y2=0，则与互相垂直．
下面四组向量：①
=（3，﹣9），
=（1，﹣
）；
②
=（2，π0），
=（2﹣1，﹣1）；
③
=（cos30°，tan45°），
=（sin30°，tan45°）；
④
=（
+2，
），
=（﹣2，
）．
其中互相垂直的组有（ ）
A. 1组 B. 2组 C. 3组 D. 4组
【答案】A
【解析】根据两个向量垂直的判定方法一一判断即可；
①∵3×1+（-9）×（-
）=6≠0，
∴
与
不垂直．
②∵2×2-1+π0×（-1）=0，
∴
与
垂直．
③∵cos30°×sin30°+tan45°×tan45°≠0，
∴
与
不垂直．
④∵(
+2)(﹣2)+
×
≠0，
∴
与
不垂直．
故选：A．
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
【题目】（1）整式
表示
、
两数和的平方
整式
表示、两数差的平方
仿照上例填空：整式
表示：______．
整式
表示：______．
（2）试计算、取不同数值时，及的值填入下表：
| 当 | 当 | 当 | 当 |
| ||||
|
（3）根据上表，我发现的规律______．
（4）用发现的规律计算：
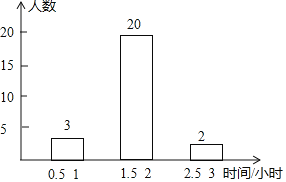
【题目】某校七年级开展了为期一周的“敬老爱亲”社会活动，并根据学生做家务的时间来评价他们在活动中的表现，学校随机抽查了部分学生在这次活动中做家务的时间，并绘制了如下的频数分布表和频数分布直方图．请根据图表中提供的信息，解答下列问题：
等级 | 做家务时间（小时） | 频数 | 百分比 |
A | 0.5≤x＜1 | 3 | 6% |
B | 1＜x＜1.5 | a | 30% |
C | 1.5≤x＜2 | 20 | 40% |
D | 2≤x＜2.5 | b | m |
E | 2.5≤x＜3 | 2 | 4% |
（1）这次活动中抽查的学生有______人，表中a=______，b=______，m=______，并补全频数分布直方图；
（2）若该校七年级有700名学生，请估计这所学校七年级学生一周做家务时间不足2小时而又不低于1小时的大约有多少人？
