题目内容
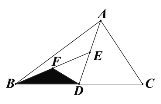
【题目】如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E,若AD=a,DE=b,
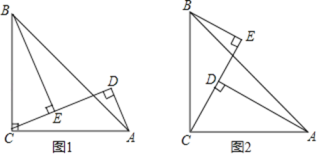
(1)如图1,求BE的长,写出求解过程;(用含a,b的式子表示)
(2)如图2,点D在△ABC内部时,直接写出BE的长___.(用含a,b的式子表示)
【答案】(1)BE=a+b;(2)BE=a-b.
【解析】
(1)先证明△BCE≌△CDA,则CE=AD=a,BE=CD=CE+ED即可算出答案.
(2)先证明△BCE≌△CDA,则CE=AD=a,BE=CD=CE-ED即可算出答案.
(1)由题意得:∠EBC+∠BCE=90°,∠BCE+∠DCA=90°,
∴∠EBC=∠DCA,
在△BCE和△CDA中
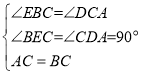
∴△BCE≌△CDA(AAS),
∴CE=AD=a,BE=CD=CE+ED=a+b.
(2) 由题意得:∠EBC+∠BCE=90°,∠BCE+∠DCA=90°,
∴∠EBC=∠DCA,
在△BCE和△CDA中
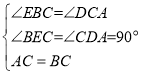
∴△BCE≌△CDA(AAS),
∴CE=AD=a,BE=CD=CE-ED=a-b.

练习册系列答案
相关题目
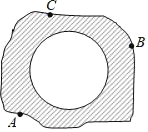
【题目】小明在操场上做游戏,他发现地上有一个不规则的封闭图形ABC.为了知道它的面积,他在封闭图形内划出了一个半径为1米的圆,在不远处向图形内掷石子,且记录如下:
掷石子次数石子落在的区域ABC | 50次 | 150次 | 300次 |
石子落在圆内(含圆上)的次数m | 14 | 43 | 93 |
石子落在阴影内的次数n | 19 | 85 | 186 |
(1)随着次数的增多,小明发现m与n的比值在一个常数k附近波动,请你写出k的值.
(2)请利用学过的知识求出封闭图形ABC的大致面积.