题目内容
(2012•襄阳)在等腰△ABC中,∠A=30°,AB=8,则AB边上的高CD的长是
或4
或4
或4
或4.
4
| ||
| 3 |
| 3 |
4
| ||
| 3 |
| 3 |
分析:此题需先根据题意画出当AB=AC时,当AB=BC时,当AC=BC时的图象,然后根据等腰三角形的性质和解直角三角形,分别进行计算即可.
解答:解:(1)当AB=AC时,
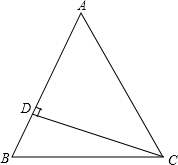
∵∠A=30°,
∴CD=
AC=
×8=4;
(2)当AB=BC时,
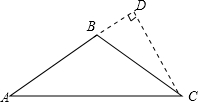
则∠A=∠ACB=30°,
∴∠ACD=60°,
∴∠BCD=30°,
∴CD=cos∠BCD•BC=cos30°×8=4
;
(3)当AC=BC时,
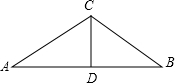
则AD=4,
∴CD=tan∠A•AD=tan30°•4=
;
故答案为:
或4
或4.

∵∠A=30°,
∴CD=
| 1 |
| 2 |
| 1 |
| 2 |
(2)当AB=BC时,

则∠A=∠ACB=30°,
∴∠ACD=60°,
∴∠BCD=30°,
∴CD=cos∠BCD•BC=cos30°×8=4
| 3 |
(3)当AC=BC时,

则AD=4,
∴CD=tan∠A•AD=tan30°•4=
4
| ||
| 3 |
故答案为:
4
| ||
| 3 |
| 3 |
点评:本题考查了等腰三角形的性质,用到的知识点是等腰三角形的性质和解直角三角形,关键是根据题意画出所有图形,要熟练掌握好边角之间的关系.

练习册系列答案
相关题目
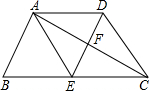 (2012•襄阳)如图,在梯形ABCD中,AD∥BC,E为BC的中点,BC=2AD,EA=ED=2,AC与ED相交于点F.
(2012•襄阳)如图,在梯形ABCD中,AD∥BC,E为BC的中点,BC=2AD,EA=ED=2,AC与ED相交于点F. (2012•襄阳)为响应市委市政府提出的建设“绿色襄阳”的号召,我市某单位准备将院内一块长30m,宽20m的长方形空地,建成一个矩形花园,要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草.如图所示,要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)
(2012•襄阳)为响应市委市政府提出的建设“绿色襄阳”的号召,我市某单位准备将院内一块长30m,宽20m的长方形空地,建成一个矩形花园,要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草.如图所示,要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形) (2012•襄阳)在一次数学活动中,李明利用一根栓有小锤的细线和一个半圆形量角器制作了一个测角仪,去测量学校内一座假山的高度CD.如图,已知小明距假山的水平距离BD为12m,他的眼镜距地面的高度为1.6m,李明的视线经过量角器零刻度线OA和假山的最高点C,此时,铅垂线OE经过量角器的60°刻度线,则假山的高度为( )
(2012•襄阳)在一次数学活动中,李明利用一根栓有小锤的细线和一个半圆形量角器制作了一个测角仪,去测量学校内一座假山的高度CD.如图,已知小明距假山的水平距离BD为12m,他的眼镜距地面的高度为1.6m,李明的视线经过量角器零刻度线OA和假山的最高点C,此时,铅垂线OE经过量角器的60°刻度线,则假山的高度为( )