Question

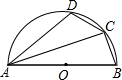（1998•海淀区）如图，四边形ABCD是圆内接四边形，AB是圆的直径，若∠BAC=20°，则∠ADC等于（　　）

A．110°

B．100°

C．120°

D．90°

Answer 1

分析：由AB是圆的直径，根据直径所对的圆周角是直角，可求得∠ACB=90°，又由∠BAC=20°，即可求得∠B的度数，然后由圆的内接四边新的性质，即可求得∠ADC的度数．

解答：解：∵AB是圆的直径，
∴∠ACB=90°，
∵∠BAC=20°，
∴∠B=90°-∠BAC=70°，
∵四边形ABCD是圆内接四边形，
∴∠ADC=180°-∠B=110°．
故选A．

点评：此题考查了圆周角定理与圆的内接四边形的性质．此题难度不大，注意掌握数形结合思想的应用．