题目内容
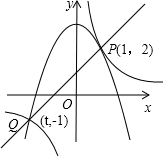如图，二次函数
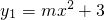的图象与反比例函数
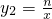的图象交于P（1，2）和Q（t，-1），直线y3=kx+b经过点P，Q．则可得不等式组：
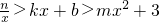的解为________．
x＜-2
分析：先根据点P的坐标求出反比例函数的解析式，再求出点Q的坐标，然后根据图象，写出反比例函数图象在直线上方，直线在二次函数图象上方部分的x的取值范围即可．
解答：∵点P（1，2）在y2=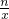
上，
∴
=2，
解得n=2，
所以，y2=
，
∵点Q在反比例函数图象上，
∴
=-1，
解得t=-2，
∴点Q的坐标为（-2，-1），
由图可知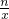，＞kx+b＞mx2+3的解是x＜-2．
故答案为：x＜-2．
点评：本题考查了二次函数与不等式组，求出点Q的坐标是解题的关键，此类题目利用数形结合确定x的范围是常用的方法．
分析：先根据点P的坐标求出反比例函数的解析式，再求出点Q的坐标，然后根据图象，写出反比例函数图象在直线上方，直线在二次函数图象上方部分的x的取值范围即可．
解答：∵点P（1，2）在y2=
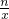上，∴
=2，解得n=2，
所以，y2=
，∵点Q在反比例函数图象上，
∴
=-1，解得t=-2，
∴点Q的坐标为（-2，-1），
由图可知，
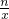＞kx+b＞mx2+3的解是x＜-2．故答案为：x＜-2．
点评：本题考查了二次函数与不等式组，求出点Q的坐标是解题的关键，此类题目利用数形结合确定x的范围是常用的方法．
练习册系列答案
相关题目
的图象，其顶点坐标为M(1,-4).
轴的交点A,B的坐标； 
,若存在，求出P点的坐标；若不存在，请说明理由；
与此图象有两个公共点时，
的取值范围.
