题目内容
矩形的两条对角线的夹角为60°，较短的一边长1cm，则较长的一边长
cm．
| 3 |
| 3 |
分析：根据题意，画出图形，首先根据矩形的对角线相等且互相平分可得AO=BO，又有条件夹角为60°，可得△AOB为等边三角形，进而得到AC的长，再利用勾股定理可以求出BC的长度．
解答：解：∵ABCD为矩形，
∴OA=OB，
∵两对角线的夹角为60°，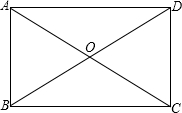
∴△AOB为等边三角形，
∴OA=OB=AB=1cm，
∴AC=BD=2cm，
∴CB=
=
=
（cm），
故答案为
．
∴OA=OB，
∵两对角线的夹角为60°，
∴△AOB为等边三角形，
∴OA=OB=AB=1cm，
∴AC=BD=2cm，
∴CB=
| AC2-AB2 |
| 4-1 |
| 3 |
故答案为
| 3 |
点评：本题主要考查矩形的基本性质：对角线相等且互相平分．熟练掌握矩形的性质是解决此类问题的基本要求．
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
矩形的两条对角线所夹的一个锐角为60°，那么矩形较短边与较长边的比是（ ）
| A、1：2 | ||
B、
| ||
C、
| ||
| D、1：3 |
，较短的边长为12，则对角线长为 。
，较短的边长为12，则对角线长为
。