题目内容
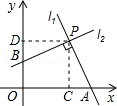
如图，P点坐标为(3，3)，l1⊥l2，l1、l2分别交x轴和y轴于A点和B点，则四边形OAPB的面积为___________．
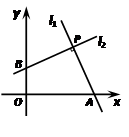
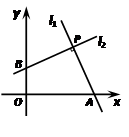
9
过P分别作x轴和y轴的垂线，交x轴和y轴于点C和D．∵P点坐标为（3，3），∴PC=PD；
又∵l1⊥l2，∴∠BPA=90°；又∵∠DPC=90°，∴∠DPB=∠PCA，△PDB≌△PCA（ASA），∴S△DPB=S△PCA，
S四边形OAPB=S正方形ODPC+S△PCA﹣S△DPB，即S四边形OAPB=S正方形ODPC=3×3=9．
又∵l1⊥l2，∴∠BPA=90°；又∵∠DPC=90°，∴∠DPB=∠PCA，△PDB≌△PCA（ASA），∴S△DPB=S△PCA，
S四边形OAPB=S正方形ODPC+S△PCA﹣S△DPB，即S四边形OAPB=S正方形ODPC=3×3=9．
练习册系列答案
相关题目
轴，则点B的坐标是 ．
