��Ŀ����
����Ŀ����֪���κ���y=��x2+bx+c+1��
����b=1ʱ����������κ����ĶԳ���ķ��̣�
����c=![]() b2��2b���ʣ�bΪ��ֵʱ�����κ�����ͼ����x�����У�
b2��2b���ʣ�bΪ��ֵʱ�����κ�����ͼ����x�����У�
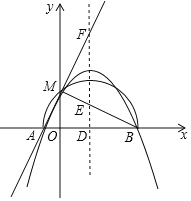
�������κ�����ͼ����x�ύ�ڵ�A��x1��0����B��x2��0������x1��x2����y��������ύ�ڵ�M����ABΪֱ���İ�Բǡ�ù���M�����κ����ĶԳ���l��x�ᡢֱ��BM��ֱ��AM�ֱ��ڵ�D��E��F��������![]() ������κ����ı���ʽ��
������κ����ı���ʽ��
���𰸡���.���κ����ĶԳ���ķ���Ϊx=![]() �� ��.bΪ2+
�� ��.bΪ2+![]() ��2��
��2��![]() ʱ�����κ�����ͼ����x����������. ���κ����ı���ʽΪy=��x2+
ʱ�����κ�����ͼ����x����������. ���κ����ı���ʽΪy=��x2+![]() x+1��
x+1��
��������
��������������κ���y=��x2+bx+c+1�ĶԳ���Ϊx=![]() �����ɵó��𰸣������κ���y=��x2+bx+c+1�Ķ�������Ϊ��
�����ɵó��𰸣������κ���y=��x2+bx+c+1�Ķ�������Ϊ��![]() ��
��![]() ����y�ɶ��κ�����ͼ����x��������c=
����y�ɶ��κ�����ͼ����x��������c=![]() b2��2b���ó�������
b2��2b���ó�������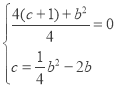 �����b���ɣ�����Բ�ܽǶ����ó���AMB=90�㣬֤����OMA=��OBM���ó���OAM�ס�OMB���ó�OM2=OAOB���ɶ��κ�����ͼ����x��Ľ������ϵ����ϵ�ó�OA=��x1��OB=x2��x1+x2��=b��x1x2=����c+1�����ó����̣�c+1��2=c+1���ó�c=0��OM=1��֤����BDE�ס�BOM����AOM�ס�ADF���ó�
�����b���ɣ�����Բ�ܽǶ����ó���AMB=90�㣬֤����OMA=��OBM���ó���OAM�ס�OMB���ó�OM2=OAOB���ɶ��κ�����ͼ����x��Ľ������ϵ����ϵ�ó�OA=��x1��OB=x2��x1+x2��=b��x1x2=����c+1�����ó����̣�c+1��2=c+1���ó�c=0��OM=1��֤����BDE�ס�BOM����AOM�ס�ADF���ó�![]() ��
��![]() ���ó�OB=4OA����x2=��4x1����x1x2=����c+1��=��1���ó�������
���ó�OB=4OA����x2=��4x1����x1x2=����c+1��=��1���ó�������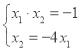 ���ⷽ�������b��ֵ���ɣ�
���ⷽ�������b��ֵ���ɣ�
��������������κ���y=��x2+bx+c+1�ĶԳ���Ϊx=![]() ����b=1ʱ��
����b=1ʱ��![]() =
=![]() ��
��
����b=1ʱ����������κ����ĶԳ���ķ���Ϊx=![]() ��
��
�����κ���y=��x2+bx+c+1�Ķ�������Ϊ��![]() ��
��![]() ����
����
�����κ�����ͼ����x��������c=![]() b2��2b��
b2��2b��
��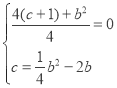 ����ã�b=2+
����ã�b=2+![]() ��b=2��
��b=2��![]() ��
��
��bΪ2+![]() ��2��
��2��![]() ʱ�����κ�����ͼ����x�����У�
ʱ�����κ�����ͼ����x�����У�
�ۡ�AB�ǰ�Բ��ֱ�������AMB=90�㣬���OAM+��OBM=90�㣬
�ߡ�AOM=��MOB=90�㣬���OAM+��OMA=90�㣬���OMA=��OBM��
���OAM�ס�OMB����![]() ����OM2=OAOB��
����OM2=OAOB��
�����κ�����ͼ����x�ύ�ڵ�A��x1��0����B��x2��0����
��OA=��x1��OB=x2��x1+x2��=b��x1x2=����c+1������OM=c+1������c+1��2=c+1��
��ã�c=0��c=��1����ȥ������c=0��OM=1��
�����κ����ĶԳ���l��x�ᡢֱ��BM��ֱ��AM�ֱ��ڵ�D��E��F��������![]() ��
��
��AD=BD��DF=4DE��DF��OM�����BDE�ס�BOM����AOM�ס�ADF��
��![]() ����DE=
����DE=![]() ��DF=
��DF=![]() ����
����![]() ��4����OB=4OA����x2=��4x1��
��4����OB=4OA����x2=��4x1��
��x1x2=����c+1��=��1����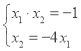 ����ã�
����ã�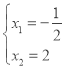 ����b=��
����b=��![]() +2=
+2=![]() ��
��
�����κ����ı���ʽΪy=��x2+![]() x+1��
x+1��

����Ŀ��ij�������10��ѧ�������ߣ����ǵ��������Ӧ���������±���ʾ
���ߣ�cm�� | 163 | 165 | 170 | 172 | 173 |
ѧ���������ˣ� | 1 | 2 | 3 | 2 | 2 |
����10��ѧ�����ߵ���������λ���ֱ�Ϊ��������
A.165cm��165cmB.170cm��165cm
C.165cm��170cmD.170cm��170cm
����Ŀ������������ӳ���ѵ������Ҫ��Ŀ֮һ������ͼ���е������Ǽס��ҡ�������ÿ��ʮ�ε�����Եijɼ������Թ���Ϊ��������10����ÿ����λ1����1�֣�
�˶�Ա�ײ��Գɼ���
������� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
�ɼ����֣� | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |

��1��д���˶�Ա�ײ��Գɼ�����������λ����
��2��������������ѡ��һλ����ɼ������ҽ�Ϊ�ȶ��Ľ���������Ϊ�����ˣ�����Ϊѡ˭������?Ϊʲô? (�ο����ݣ����˳ɼ��ķ���ֱ�Ϊ![]() ��
��![]() ��
��![]() )
)
��3���ס��ҡ��������֮����е�����ϰ��ÿ���˵��ȿ��ܵĴ����������ˣ������ȴӼ����д����������ֽ���ʱ��ص������еĸ����Ƕ��٣�������״ͼ���б������
����Ŀ���Ķ����в��ϣ�
���⣺ij���깤����Ա��һ������13ֻ����5ֻѼ��9ֻ�칲����925Ԫ���ڶ�������2ֻ����4ֻѼ��3ֻ�칲����320Ԫ�����ʵ��������˼���Ѽ�����һֻ�������Ԫ��(�ٶ����ι���Ѽ����ĵ��۲���)
�⣺�輦��Ѽ����ĵ��۷ֱ�Ϊx��y��zԪ�������⣬��![]()
����������ɱ���Ϊ![]()
��x��y��z��a��2x��z��b������������ɻ�Ϊ��![]()
����4���ڵã�a��____����x��y��z��____��
�𣺵�������Ѽ�����һֻ����____Ԫ��
�Ķ���ϸ�ĵ��㣬���Խ���������⣺(1)����������a�� ��
(2)ѡ���⣺���������еĽ����������� ˼�뷽����ָ�����⣮
A������ B������ C����������
(3)ijУ�����鹺��������Ʒ�ס��ҡ��������ļ�������Ǯ������±���
������Ʒ�� ���������� | �� | �� | �� | �� | ��Ǯ���(Ԫ) |
��һ�ι������ | 5 | 4 | 3 | 1 | 1 882 |
�ڶ��ι������ | 9 | 7 | 5 | 1 | 2 764 |
��ô����ÿ��������Ʒ��һ���������Ԫ��