题目内容
（2002•兰州）已知如图⊙O1与⊙O2交于A、B，P、Q为⊙O1上两点，PA的延长线交⊙O2于M，PB交⊙O2于F，QA、QB的延长线交⊙O2于E、N．求证：EF∥MN．
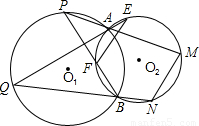
【答案】分析：连接AB，EN，可以证明△AQB∽△NQE，把证明EF∥MN的问题转化为证明∠ENM=∠NEF．
解答：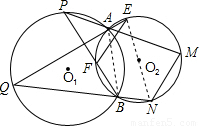
证明：连接AB，EN，
∵QA•QE=QB•QN，
=
，
∵∠AQB=∠NQE，
∴△AQB∽△NQE．
∴∠QBA=∠QEN．
又∵∠QBA=∠QBP+∠FBA，∠QEN=∠FEN+∠FEA，
又∵∠NEF=∠QAP，∠QAP=∠EAM，∠EAM=∠ENM，
∴∠ENM=∠NEF．
∴EF∥MN．
点评：本题考查切割线定理，相似三角形的性质及圆周角定理等的综合运用．
解答：
证明：连接AB，EN，∵QA•QE=QB•QN，
=，∵∠AQB=∠NQE，
∴△AQB∽△NQE．
∴∠QBA=∠QEN．
又∵∠QBA=∠QBP+∠FBA，∠QEN=∠FEN+∠FEA，
又∵∠NEF=∠QAP，∠QAP=∠EAM，∠EAM=∠ENM，
∴∠ENM=∠NEF．
∴EF∥MN．
点评：本题考查切割线定理，相似三角形的性质及圆周角定理等的综合运用．
练习册系列答案
相关题目
（k≠0）和一次函数y=-x+8．