题目内容
【题目】如图:△ABC中,![]() ACB=90°,AC=BC,AB=4,点E在BC上,且BE=2,点P在
ACB=90°,AC=BC,AB=4,点E在BC上,且BE=2,点P在![]() ABC的平分线BD上运动,则PE+PC的长度最小值为()
ABC的平分线BD上运动,则PE+PC的长度最小值为()
A.1
B.![]()
C.![]()
D.![]()
【答案】B
【解析】作点E关于BD的对称点E',连接E'C,如下图: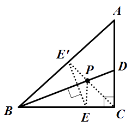
∵BD是∠ ABC的平分线,
∴通过作图知,BP垂直平分EE',
∴PE'=PE
∴此时PE+PC=PE'+PC=E'C,PE+PC的长度最小,
∵点E、点E'关于BD的对称,∴BE'=BE=2,
又∵AB=4,∴点E'是AB中点,CE'是中线.
∵△ABC中, ∠ ACB=90°,AC=BC,
∴△ABC是等腰直角三角形,∠ ABC=45![]() ,
,
∴CE'又是底边AB的高,
∴△BE'C也是等腰直角三角形,
∴E'C=2,
即:PE+PC的长度最小值为2.
故选B.
【考点精析】根据题目的已知条件,利用三角形的“三线”和轴对称-最短路线问题的相关知识可以得到问题的答案,需要掌握1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内;已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
