题目内容
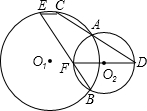如图，已知⊙O1和⊙O2相交于点A、B，过点A作直线分别交⊙O1、⊙O2于点C、D，过点B作直线分别交⊙O1、⊙O2于点E、F，求证：CE∥DF．分析：连接AB，根据圆周角定理易证∠E=∠DFB，然后根据平行线的判定定理即可证明．
解答：证明：连接AB．
∵A、B、E、C在⊙O1上，
∴∠DAB=∠E，
又∵A、D、B、F在⊙O2上，
∴∠DAB=∠DFB．
∴∠E=∠DFB，
∴CE∥DF．
∵A、B、E、C在⊙O1上，
∴∠DAB=∠E，
又∵A、D、B、F在⊙O2上，
∴∠DAB=∠DFB．
∴∠E=∠DFB，
∴CE∥DF．
点评：本题考查了圆周角定理，理解定理是关键．
练习册系列答案
作业辅导系列答案
同步学典一课多练系列答案
经典密卷系列答案
金牌课堂练系列答案
相关题目
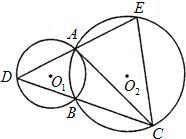21、如图，已知⊙O1和⊙O2相交于A，B两点，过点A作⊙O1的切线交⊙O2于点C，直线CB交⊙O1于点D，直线DA交⊙O2于点E．试证明：AC=EC．
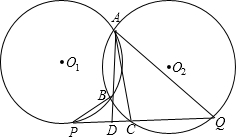求S△ADC：S△ACQ的值．
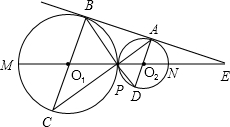长线交⊙O1于C点，BP的延长线交⊙O2于D点，直线O1O2交⊙O1于M，交⊙O2于N，与BA的延长线交于点E．
时它与⊙O1的位置关系是