题目内容
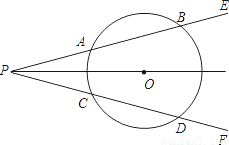
39、如图,点O是∠EPF的平分线上的一点,以O为圆心的圆和角的两边分别交于点A,B和C,D,
(1)AB和CD相等吗?为什么?
(2)若角的顶点P在圆上,或在圆内,本题的结论是否成立?请说明理由.
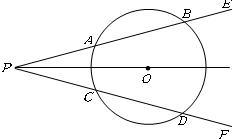
(1)AB和CD相等吗?为什么?
(2)若角的顶点P在圆上,或在圆内,本题的结论是否成立?请说明理由.

分析:(1)分别过O作OG⊥AB,OH⊥CD,根据角平分线定理得到OG=OH,然后由垂径定理可以得到AB=CD;
(2)根据题意画出点P在圆上和圆内的情况,根据垂径定理可以证明结论成立.
(2)根据题意画出点P在圆上和圆内的情况,根据垂径定理可以证明结论成立.
解答:解:(1)相等.
如图:
作OG⊥AB于G,OH⊥CD于H,AG=BG,CH=DH,
∵∠EPO=∠FPO,
∴OG=OH.
在Rt△OBG和Rt△ODH中,
由HL定理得:△OBG≌△ODH,
∴GB=HD,
∴AB=CD;
(2)点P在圆上,或在圆内,结论成立.
如图1:
顶点P在圆上,此时点P,A,C重合于点A,作OG⊥AB于G,OH⊥AD于H,
∴AG=GB,AH=HD,
∵∠EAO=∠DAO,
∴OG=OH.
在Rt△OAG和Rt△OAH中,由HL定理得:△OAG≌△OAH,
∴AG=AH,
∴AB=AD.
即点P在圆上,结论成立.
如图2:
顶点P在圆内,作OG⊥AB于G,OH⊥CD于H,则AG=GB,CH=HD,
∵∠EPO=∠FPO,
∴OG=OH,
∴GB=HD,
∴AB=CD.
即点P在圆内,结论成立.
如图:

作OG⊥AB于G,OH⊥CD于H,AG=BG,CH=DH,
∵∠EPO=∠FPO,
∴OG=OH.
在Rt△OBG和Rt△ODH中,
由HL定理得:△OBG≌△ODH,
∴GB=HD,
∴AB=CD;
(2)点P在圆上,或在圆内,结论成立.
如图1:

顶点P在圆上,此时点P,A,C重合于点A,作OG⊥AB于G,OH⊥AD于H,
∴AG=GB,AH=HD,
∵∠EAO=∠DAO,
∴OG=OH.
在Rt△OAG和Rt△OAH中,由HL定理得:△OAG≌△OAH,
∴AG=AH,
∴AB=AD.
即点P在圆上,结论成立.
如图2:

顶点P在圆内,作OG⊥AB于G,OH⊥CD于H,则AG=GB,CH=HD,
∵∠EPO=∠FPO,
∴OG=OH,
∴GB=HD,
∴AB=CD.
即点P在圆内,结论成立.
点评:本题考查的是垂径定理,先根据角平分线的性质定理,得到两条弦心距相等,然后再说明两条弦相等.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
 12、如图,点O是∠EPF的平分线上一点,⊙O和∠EPF的两边分别交于点A、B和C、D,根据上述条件,可以推出
12、如图,点O是∠EPF的平分线上一点,⊙O和∠EPF的两边分别交于点A、B和C、D,根据上述条件,可以推出 已知:如图,点O是∠EPF的平分线上的一点,以O为圆心的圆和角的两边分别交于点A,B和C,D.求证:AB=CD.
已知:如图,点O是∠EPF的平分线上的一点,以O为圆心的圆和角的两边分别交于点A,B和C,D.求证:AB=CD.