题目内容
如图，点O是∠EPF的平分线上一点，⊙O和∠EPF的两边分别交于点A、B和C、D，根据上述条件，可以推出 ．（要求：填写一个你认为正确的结论即可，不再标注其他字母，不写推理过程）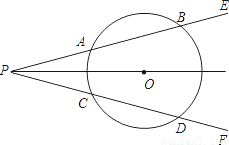
【答案】分析：先利用去全等求出OM=ON，再得AB=CD或弧AB=弧CD．
解答：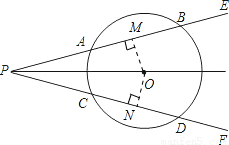
解：如图：作OM⊥AB，交AB于点M，ON⊥CD，交CD于点N，
点O是∠EPF的平分线上一点，
∴OM=ON，根据在同圆中两弦的弦心距相等，则弦长相等，
知，AB=CD，
故弧AB=弧CD．
点评：本题利用了：
（1）角的平分线的性质：角的平分线上的点到角的两边的距离相等．
（2）在同圆中两弦的弦心距相等，则弦长相等．
解答：
解：如图：作OM⊥AB，交AB于点M，ON⊥CD，交CD于点N，点O是∠EPF的平分线上一点，
∴OM=ON，根据在同圆中两弦的弦心距相等，则弦长相等，
知，AB=CD，
故弧AB=弧CD．
点评：本题利用了：
（1）角的平分线的性质：角的平分线上的点到角的两边的距离相等．
（2）在同圆中两弦的弦心距相等，则弦长相等．
练习册系列答案
相关题目
12、如图，点O是∠EPF的平分线上一点，⊙O和∠EPF的两边分别交于点A、B和C、D，根据上述条件，可以推出
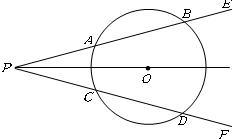
已知：如图，点O是∠EPF的平分线上的一点，以O为圆心的圆和角的两边分别交于点A，B和C，D．求证：AB=CD．