题目内容
【题目】如图,在矩形ABCD中,AB=5,AD=4,E为AD边上一动点(不与点A重合),AF⊥BE,垂足为F,GF⊥CF,交AB于点G,连接EG.设AE=x,S△BEG=y.
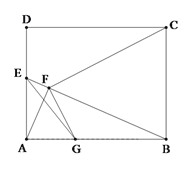
(1)证明:△AFG∽△BFC;
(2)求y与x的函数关系式,并求出y的最大值;
(3)若△BFC为等腰三角形,请直接写出x的值.
【答案】(1)证明见解析;
(2y与x的函数关系式为![]() ,y的最大值为
,y的最大值为![]() ;
;
(3)x的值为![]() ,
, ![]() 或
或![]() .
.
【解析】试题分析:(1)分别证明∠GAF=∠FBC,∠AFG=∠CFB即可证明△AFG∽△BFC;
(2)先求出AG= ![]() ,再求出BG=5-
,再求出BG=5- ![]() ,利用三角形面积公式即可得出y与x的函数关系式,从而求出结果;
,利用三角形面积公式即可得出y与x的函数关系式,从而求出结果;
(3)分情况进行讨论即可得解.
试题解析:(1)证明:在矩形ABCD中,∠ABC=90°.
∴∠ABF+∠FBC=90°.
∵AF⊥BE,
∴∠AFB=90°.
∴∠ABF+∠GAF=90°.
∴∠GAF=∠FBC.
∵FG⊥FC,
∴∠GFC=90°.
∴∠ABF=∠GFC.
∴∠ABF-∠GFB =∠GFC-∠GFB.
即∠AFG=∠CFB.
∴△AFG∽△BFC;
(2)由(1)得△AFG∽△BFC,
∴![]() .
.
在Rt△ABF中,tan∠ADF=![]() ,
,
在Rt△EAB中,tan∠EBA=![]() ,
,
∴![]() .
.
∴![]() .
.
∵BC=AD=4,AB=5,
∴![]() .
.
∴BG=AB-AG=5- ![]() .
.
∴![]() .
.
∴y的最大值为![]() ;
;
(3)x的值为![]() ,
, ![]() 或
或![]() .
.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目


