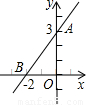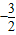题目内容
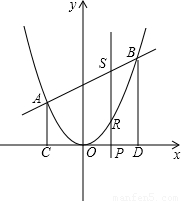
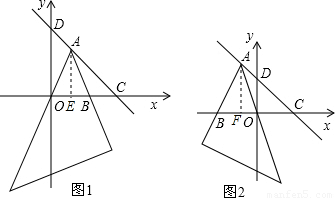
(2007•大连)如图1,直线y=-x+1与x轴、y轴分别相交于点C、D,一个含45°角的直角三角板的锐角顶点A在线段CD上滑动,滑动过程中三角板的斜边始终经过坐标原点,∠A的另一边与轴的正半轴相交于点B.(1)试探索△AOB能否构成以AO、AB为腰的等腰三角形?若能,请求出点B的坐标;若不能,说说明理由;
(2)若将题中“直线y=-x+1”、“∠A的另一边与轴的正半轴相交于点B”分别改为“直线y=-x+t(t>0)”、“∠A的另一边与轴的负半轴相交于点B”(如图2),其他条件不变,试探索△AOB能否为等腰三角形(只考虑点A在线段CD的延长线上且不包括点D时的情况)?若能,请求出点B的坐标;若不能,请说明理由.
【答案】分析:(1)先假设存在AO、AB为腰的等腰三角形.然后根据函数解析式求出C、D点坐标,判断出∠OCD=∠ODC=45,再根据角的加减法求出∠BAC=22.5°=∠DOA,进而证出△ABC≌△OAD,可得出点B的坐标为(2- ,0).
,0).
(2)若△AOB为等腰三角形,则必为一边为底,两边为腰,分以下三种情况:①OA=OB,
根据∠OBA=∠OAB=45°,推出∠AOB=90°,得出矛盾;②BA=BO,根据∠BOA=∠BAO,得OA∥CA,推出矛盾,③AB=AO,根据角的加减、线段的加减和函数解析式,求出B的坐标.
解答:解:将x=0代入y=-x+1,y=0代入y=-x+1得点C、D的坐标为(1,0)(0,1).则:
OC=OD=1,CD= ,∠OCD=∠ODC=45°,
,∠OCD=∠ODC=45°,
(1)△AOB可以构成AO、AB为腰的等腰三角形.
∵AO=AB,∠OAB=45°
∴∠AOB=∠ABO=67.5°,∠DOA=22.5°
又∵∠AOB=∠BAC+∠ACB
即67.5°=∠BAC+45°
∴∠BAC=22.5°=∠DOA
∴△ABC≌△OAD
∴AC=OD=1,BC=AD=CD-AC= ,
,
则OB=OC-BC=2- .
.
点B的坐标为(2- ,0)
,0)
即在滑动过程中△AOB可以构成以AO、AB为腰的等腰三角形,此时点B的坐标为(2- ,0)
,0)
(2)若△AOB为等腰三角形,则有如下三种情况:
①OA=OB,则∠OBA=∠OAB=45°,
因此∠AOB=90°,点A与点D重合,不合题意.
②BA=BO,则∠BOA=∠BAO,
∴OA∥CA,
因此不合题意.
③AB=AO,
∵∠BAO=45°
∴∠AOB=∠ABO=67.5°
∴∠AOD=∠BOD-∠AOB=22.5°
∴∠OAD=∠ODC-∠AOD=22.5°=∠AOD
∴∠ABC=∠BAC=67.5°
由y=-x+t知OC=OD=t,DC=
∴AD=OD=t,BC=AC=AD+DC= t+t
t+t
∴BO=BC-OC=
∴点B的坐标为(- t,0).
t,0).
点评:此题为一道开放性操作题.通过三角板的移动结合等腰三角形的性质考查了同学们的探索发现的能力,综合性较强.
 ,0).
,0).(2)若△AOB为等腰三角形,则必为一边为底,两边为腰,分以下三种情况:①OA=OB,
根据∠OBA=∠OAB=45°,推出∠AOB=90°,得出矛盾;②BA=BO,根据∠BOA=∠BAO,得OA∥CA,推出矛盾,③AB=AO,根据角的加减、线段的加减和函数解析式,求出B的坐标.
解答:解:将x=0代入y=-x+1,y=0代入y=-x+1得点C、D的坐标为(1,0)(0,1).则:
OC=OD=1,CD=
 ,∠OCD=∠ODC=45°,
,∠OCD=∠ODC=45°,(1)△AOB可以构成AO、AB为腰的等腰三角形.
∵AO=AB,∠OAB=45°
∴∠AOB=∠ABO=67.5°,∠DOA=22.5°
又∵∠AOB=∠BAC+∠ACB
即67.5°=∠BAC+45°
∴∠BAC=22.5°=∠DOA
∴△ABC≌△OAD
∴AC=OD=1,BC=AD=CD-AC=
 ,
,则OB=OC-BC=2-
 .
.点B的坐标为(2-
 ,0)
,0)即在滑动过程中△AOB可以构成以AO、AB为腰的等腰三角形,此时点B的坐标为(2-
 ,0)
,0)(2)若△AOB为等腰三角形,则有如下三种情况:
①OA=OB,则∠OBA=∠OAB=45°,
因此∠AOB=90°,点A与点D重合,不合题意.
②BA=BO,则∠BOA=∠BAO,
∴OA∥CA,
因此不合题意.
③AB=AO,
∵∠BAO=45°
∴∠AOB=∠ABO=67.5°
∴∠AOD=∠BOD-∠AOB=22.5°
∴∠OAD=∠ODC-∠AOD=22.5°=∠AOD
∴∠ABC=∠BAC=67.5°
由y=-x+t知OC=OD=t,DC=

∴AD=OD=t,BC=AC=AD+DC=
 t+t
t+t∴BO=BC-OC=

∴点B的坐标为(-
 t,0).
t,0).点评:此题为一道开放性操作题.通过三角板的移动结合等腰三角形的性质考查了同学们的探索发现的能力,综合性较强.

练习册系列答案
相关题目