题目内容
 (2002•淮安)(1)已知关于x的方程x2-2ax+a2-2a+2=0的两个实数根x1,x2满足x12+x22=2,求a的值.
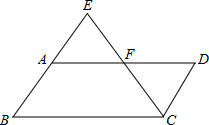
(2002•淮安)(1)已知关于x的方程x2-2ax+a2-2a+2=0的两个实数根x1,x2满足x12+x22=2,求a的值.(2)如图,在平行四边形ABCD中,延长BA至E,使AE=AB,连接CE交AD于F点,
①求证:AF=DF;
②若SABCD=12,求S△AEF.
分析:(1)根据根与系数的关系得出x1+x2=2a,x1•x2=a2-2a+2,代入(x1+x2) 2-2x1•x2=2,得出一个关于a的方程,求出方程的解即可;
(2)①推出AB=CD,AB∥CD,推出AE=CD,证△EAF与△CDF全等即可;②过C作CM⊥AD于M,得出AB×CM=12,根据三角形的面积公式求出即可.
(2)①推出AB=CD,AB∥CD,推出AE=CD,证△EAF与△CDF全等即可;②过C作CM⊥AD于M,得出AB×CM=12,根据三角形的面积公式求出即可.
解答:(1)解:根据根与系数的关系得:x1+x2=2a,x1•x2=a2-2a+2,
∵x12+x22=2,
∴(x1+x2) 2-2x1•x2=2,
即4a2-2(a2-2a+2)=2,
解得:a1=-3,a2=1.
即a的值是-3或1.
(2)①证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵AB=AE,
∴AE=CD,
∵AB∥CD,
∴∠E=FCD,∠D=∠EAF,
在△EAF和△CDF中
,
∴△EAF≌△CDF,
∴AF=DF.
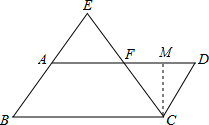
②解:过C作CM⊥AD于M,
∵SABCD=12,
∴AD×CM=12,
∴S△AEF=S△DCF=
DF×CM=
×
AB×CM=
×12=3,
即S△AEF=3.
∵x12+x22=2,
∴(x1+x2) 2-2x1•x2=2,
即4a2-2(a2-2a+2)=2,
解得:a1=-3,a2=1.
即a的值是-3或1.
(2)①证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵AB=AE,
∴AE=CD,
∵AB∥CD,
∴∠E=FCD,∠D=∠EAF,
在△EAF和△CDF中
|
∴△EAF≌△CDF,
∴AF=DF.

②解:过C作CM⊥AD于M,
∵SABCD=12,
∴AD×CM=12,
∴S△AEF=S△DCF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
即S△AEF=3.
点评:本题考查了平行四边形的性质和判定,根与系数的关系,全等三角形的性质和判定的应用,主要考查学生运用性质进行推理和计算的能力,注意:x1+x2=2a,x1•x2=a2-2a+2.

练习册系列答案
相关题目