��Ŀ����
ij�̳�����һ������Ʒ,ÿ��������120Ԫ���������ڼ䷢�֣���ÿ����Ʒ�ۼ�130Ԫʱ��ÿ�������70������ÿ����Ʒ�۸ߣ���ͣ���130Ԫʱ��ÿ��(��)��1Ԫ�����������ͼ��٣������ӣ�1��.�ݴ˹��ɣ���ش�
�ŵ�ÿ����Ʒ�ۼ۶�Ϊ170Ԫʱ��ÿ������۶��ټ���Ʒ���̳���õ���ӯ���Ƕ��٣�
���������������䣬��Ʒ��������������£�ÿ����Ʒ�����ۼ۶�Ϊ����Ԫʱ���̳���ӯ���ɴﵽ1600Ԫ������ʾ��ӯ��=�ۼۡ����ۣ�
�ŵ�ÿ����Ʒ�ۼ۶�Ϊ170Ԫʱ��ÿ������۶��ټ���Ʒ���̳���õ���ӯ���Ƕ��٣�
���������������䣬��Ʒ��������������£�ÿ����Ʒ�����ۼ۶�Ϊ����Ԫʱ���̳���ӯ���ɴﵽ1600Ԫ������ʾ��ӯ��=�ۼۡ����ۣ�
��1����ÿ����Ʒ�ۼ۶�Ϊ170Ԫʱ��ÿ�������30����Ʒ���̳���õ���ӯ����1500Ԫ��
��2��ÿ����Ʒ�����ۼ۶�Ϊ160Ԫ�����ӯ����1600Ԫ��
��2��ÿ����Ʒ�����ۼ۶�Ϊ160Ԫ�����ӯ����1600Ԫ��
�����������1���������ÿ���������Ʒ������Ȼ��������ӯ����
��2�������̳���ӯ���ﵽ1600Ԫʱ��ÿ����Ʒ�ۼ�ΪxԪ������ÿ����Ʒ��ӯ�������۵ļ���=�̳�����ӯ�����з�����⼴�ɣ�
�ڸ��ݢ������й�ϵʽ�������ó�ӯ�����ۼ�֮��Ĺ�ϵ���������ö��κ�����ֵ��������ɣ�
�����������1����ÿ����Ʒ�ۼ�Ϊ170Ԫʱ����ÿ����Ʒ�ۼ�130Ԫ�߳�40Ԫ��
��170��130=40��Ԫ����
��ÿ���������Ʒ30������70��40=30��������
�̳��ɻ���ӯ��Ϊ��170��120����30=1500��Ԫ����
��ÿ�������30����Ʒ���̳���õ���ӯ����1500Ԫ��
��2�������̳���ӯ���ﵽ1600Ԫʱ��ÿ����Ʒ�ۼ�ΪxԪ��
��ÿ����Ʒ��130Ԫ�߳���x��130��Ԫ��ÿ����ӯ����x��120��Ԫ��
ÿ��������ƷΪ70����x��130��=200��x��������
������÷��̣�200��x����x��120��=1600��
��������x2��320x+25600=0����
��x��160��2=0��
��ã�x=160��
��ÿ����Ʒ�ۼ�Ϊ160Ԫʱ���̳���ӯ���ﵽ1600Ԫ��
�������Ʒ��ӯ��ΪyԪ��������ã�
y=��200��x����x��120��
=��x2+320x��24000
=����x2��320x����24000
=����x��160��2+1600��
��ÿ����Ʒ�����ۼ۶�Ϊ160Ԫ�����ӯ����1600Ԫ��

��ϰ��ϵ�д�
 ���Ӣ��������ϵ�д�
���Ӣ��������ϵ�д�
�����Ŀ

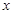 �ķ���
�ķ���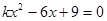 ��ʵ��������
��ʵ��������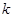 ��ȡֵ��Χ�� ��
��ȡֵ��Χ�� ��



 ��
�� ��һԪ���η���
��һԪ���η��� ������������
������������ ��ֵ�ǣ� ��.
��ֵ�ǣ� ��.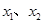 ,��ô
,��ô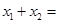 _______��
_______��