Question

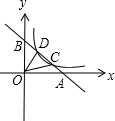如图，已知直线y=-x+3与坐标轴交于A、B两点，与双曲线y=

k

x

交于C、D两点，且S_△AOC=S_△COD
=S_△BOD，则k=

 

．

Answer 1

分析：先由已知：S_△AOC=S_△COD=S_△BOD得出AC=CD=DB，求出点C的横坐标，再由已知和：S_△AOC=S_△COD=S_△BOD求出∴S_△AOC的面积，继而求出点C的纵坐标，从而求出k的值

解答：解：已知：S_△AOC=S_△COD=S_△BOD，
∴AC=CD=DB，
∴C、D为AB的三等分点，
又由直线y=-x+3与坐标轴交于A、B两点，
∴得：A点的坐标为：（3，0），B点的坐标为：（0，3），
∴点C的横坐标为：2，
∴S_△AOB=

1

2

×3×3=

9

2

，
∴S_△AOC=

1

3

S_△AOB=

1

3

×

9

2

=

3

2

，
设点C的纵坐标为y，
则

1

2

×3×y=

3

2

，
∴y=1，
又点C在双曲线y=

k

x

上，
∴1=

k

2

，
∴k=2，
故答案为：2．

点评：本题考查了反比例函数的应用，解题的关键是根据双曲线上点的坐标特点，根与系数关系，三角形面积的表示方法，通过代数变形，得出已知三角形与所求三角形的面积关系．