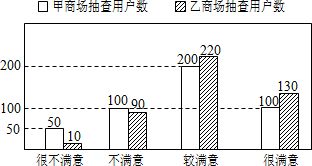
题目内容
计算:
(1)[(x+y)2-y(2x+y)-8x]÷2x;
(2)已知:m-n=4,m2-n2=24,求(m+n)3的值.
(3)已知-2x3m+1y2n与7xn-6y-3-m的积与x4y是同类项,求m2+n的值.
(4)先化简,再求值:(-2a4x2+4a3x3- a2x4)÷(-a2x2),其中a=
a2x4)÷(-a2x2),其中a= ,x=-4.
,x=-4.
(5)分解因式:
①(x+y)2-9y2;
②10b(x-y)2-5a(y-x)2;
③(ab+b)2-(a+1)2;
解:(1)[(x+y)2-y(2x+y)-8x]÷2x=(x2+2xy+y2-2xy-y2-8x)÷2x=(x2-8x)÷2x=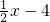 ;
;
(2)∵m-n=4,m2-n2=24,
∵m2-n2=(m-n)(m+n)=4(m+n)=24,
∴m+n=6,
∴(m+n)3,=63=216;
(3)-2x3m+1y2n•7xn-6y-3-m=-14x3m+n-5y2n-3-m;
∵-2x3m+1y2n与7xn-6y-3-m的积与x4y是同类项,
∴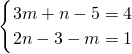 ,
,
解得: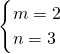 ,
,
∴m2+n=22+3=7;
(4)(-2a4x2+4a3x3- a2x4)÷(-a2x2)=2a2-4ax+
a2x4)÷(-a2x2)=2a2-4ax+ x2,
x2,
当a= ,x=-4时,原式=2×(
,x=-4时,原式=2×( )2-4×
)2-4× ×(-4)+
×(-4)+ ×(-4)2=
×(-4)2=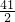 ;
;
(5)①(x+y)2-9y2=(x+y+3y)(x+y-3y)=(x+4y)(x-2y);
②10b(x-y)2-5a(y-x)2=10b(x-y)2-5a(x-y)2=5(x-y)2(2b-a);
③(ab+b)2-(a+1)2=(ab+b+a+1)(ab+b-a-1).
分析:(1)利用整式的混合运算,首先算括号里,再利用多项式除以单项式法则求解即可;
(2)利用平方差公式,求得(m+n)的值,代入即可求得结果;
(3)根据同类项的知识,列得方程组,解方程组求得m与n的值,代入即可求得结果;
(4)首先利用多项式除以单项式的法则化简代数式,再代入求值即可;
(5)利用平方差公式分解,注意分解要彻底.
点评:此题考查了多项式除以单项式的知识,以及因式分解等知识.注意化简求值的题目,需要先化简再求值;因式分解的题目要注意:先找公因式,再利用公式分解,分解要彻底.
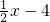 ;
;(2)∵m-n=4,m2-n2=24,
∵m2-n2=(m-n)(m+n)=4(m+n)=24,
∴m+n=6,
∴(m+n)3,=63=216;
(3)-2x3m+1y2n•7xn-6y-3-m=-14x3m+n-5y2n-3-m;
∵-2x3m+1y2n与7xn-6y-3-m的积与x4y是同类项,
∴
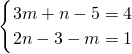 ,
,解得:
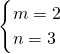 ,
,∴m2+n=22+3=7;
(4)(-2a4x2+4a3x3-
 a2x4)÷(-a2x2)=2a2-4ax+
a2x4)÷(-a2x2)=2a2-4ax+ x2,
x2,当a=
 ,x=-4时,原式=2×(
,x=-4时,原式=2×( )2-4×
)2-4× ×(-4)+
×(-4)+ ×(-4)2=
×(-4)2=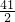 ;
;(5)①(x+y)2-9y2=(x+y+3y)(x+y-3y)=(x+4y)(x-2y);
②10b(x-y)2-5a(y-x)2=10b(x-y)2-5a(x-y)2=5(x-y)2(2b-a);
③(ab+b)2-(a+1)2=(ab+b+a+1)(ab+b-a-1).
分析:(1)利用整式的混合运算,首先算括号里,再利用多项式除以单项式法则求解即可;
(2)利用平方差公式,求得(m+n)的值,代入即可求得结果;
(3)根据同类项的知识,列得方程组,解方程组求得m与n的值,代入即可求得结果;
(4)首先利用多项式除以单项式的法则化简代数式,再代入求值即可;
(5)利用平方差公式分解,注意分解要彻底.
点评:此题考查了多项式除以单项式的知识,以及因式分解等知识.注意化简求值的题目,需要先化简再求值;因式分解的题目要注意:先找公因式,再利用公式分解,分解要彻底.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目