题目内容
(1)如图,边长为1的五个小正方形恰好如图放在大正方形中,求大正方形的边长.

(2)如图,六个大小完全一样的小正方形如图放置在大正方形中,已知大正方形的边长是10,求图中x的值.

 解:(1)大正方形中,∠A=∠D=∠F=90°,AD=DF,
解:(1)大正方形中,∠A=∠D=∠F=90°,AD=DF,∵∠1+∠DCE=90°,∠2+∠DCE=90°,
∴∠1=∠2,
∴△ABC∽△DCE,
∵四边形BCEG由边长为1的五个小正方形组成,
∴BC=EG=1,EC=5,
∴
 ,
,∴DE=5AC,DC=5AB,
同理得∠2=∠3,
∴∠1=∠3,
在△ABC和△FEG中,
 ,
,∴△ABC≌△FEG(AAS),
∴AC=FG,AB=FE,
∵AC+CD=DE+EF,
∴AC+5AB=5AC+AB,
∴AB=AC,
∴∠1=45°,
∴AB=AC=BC•sin∠1=1×
 =
= ,
,∴AD=6AC=6×
 =
= ;
;(2)解:如图示,

∵正方形ABCD边长为10,
∴∠A=∠B=90°,AB=10,
过点E作EF⊥BC,垂足为F,则∠4=∠5=90°,
∴四边形AEFB是矩形,
∴∠2+∠3=90°,EF=AB=10,
∵六个大小完全一样的小正方形如图放置在大正方形中,
∴∠1+∠2=90°,
∴∠1=∠3,
∴△AEG∽△FEH,
∴
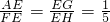 ,
,∴
 ,
,∴X=2.
分析:(1)根据正方形的角都是直角和同角的余角相等,求出∠1=∠2,所以△ABC∽△DCE,根据相似三角形对应边成比例求出DE=5AC,DC=5AB,同理∠2=∠3,又BC=EG,所以△ABC≌△FEG,AC=FG,AB=FE,再根据大正方形的边长相等列式整理即可得到AB=AC,所以△ABC为等腰直角三角形,求出AB的长度,大正方形的边长为6AB;
(2)如图,过E作EF⊥BC,垂足为F,可以得到△AEG∽△FEH,再根据相似三角形对应边成比例的性质列式求解即可得到x.
点评:本题主要利用三角形全等的判定和全等三角形的性质,相似三角形的判定和相似三角形对应边成比例的性质,综合性较强.

练习册系列答案
相关题目
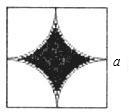 如图,边长为a的正方形中,阴影部分的面积是( )
如图,边长为a的正方形中,阴影部分的面积是( )| A、a2-πa2 | ||
| B、πa2-a2 | ||
C、a2-π(
| ||
| D、(a-π)2 |
 如图.边长为1的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A顺时针旋转45°,则这两个正方形重叠部分的面积是
如图.边长为1的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A顺时针旋转45°,则这两个正方形重叠部分的面积是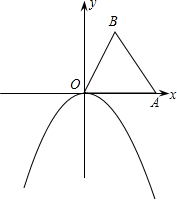 点A落在抛物线y=ax2(a<0)的图象上.
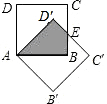
点A落在抛物线y=ax2(a<0)的图象上. (2012•金牛区二模)如图,边长为2的正方形ABCD绕点A逆时针旋转45度后得到正方形AB′C′D′,边B′C′与DC交于点O,则四边形AB′OD的周长是( )
(2012•金牛区二模)如图,边长为2的正方形ABCD绕点A逆时针旋转45度后得到正方形AB′C′D′,边B′C′与DC交于点O,则四边形AB′OD的周长是( ) 如图:边长为12的大正方形中有两个小正方形,若两个小正方形的面积分别为S1、S2,则S1+S2的值为( )
如图:边长为12的大正方形中有两个小正方形,若两个小正方形的面积分别为S1、S2,则S1+S2的值为( )