题目内容
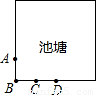
 如图:边长为12的大正方形中有两个小正方形,若两个小正方形的面积分别为S1、S2,则S1+S2的值为( )
如图:边长为12的大正方形中有两个小正方形,若两个小正方形的面积分别为S1、S2,则S1+S2的值为( )分析:由图可得,S1的边长为6,由AC=
BC,BC=CE=
CD,可得AC=2CD,CD=4,EC=4
然后,分别算出S1、S2的面积,即可解答.
| 2 |
| 2 |
| 2 |
解答: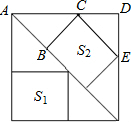 解:如图,设正方形S2的边长为x,
解:如图,设正方形S2的边长为x,
根据等腰直角三角形的性质知,AC=
x,x=
CD,
∴AC=2CD,CD=4,
∴EC2=42+42,即EC=4
,
∴S2的面积为EC2=32,
∵S1的边长为6,S1的面积为6×6=36,
∴S1+S2=32+36=68.
故选C.
 解:如图,设正方形S2的边长为x,
解:如图,设正方形S2的边长为x,根据等腰直角三角形的性质知,AC=
| 2 |
| 2 |
∴AC=2CD,CD=4,
∴EC2=42+42,即EC=4
| 2 |
∴S2的面积为EC2=32,
∵S1的边长为6,S1的面积为6×6=36,
∴S1+S2=32+36=68.
故选C.
点评:本题考查了正方形的性质和等腰直角三角形的性质以及勾股定理的运用,同时也考查了学生的读图能力.

练习册系列答案
相关题目
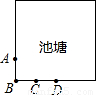
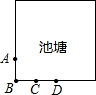 如图,边长为12米的正方形池塘的周围是草地,池塘边A、B、C、D处各有一棵树,且AB=BC=CD=3米.现用长4米的绳子将一头羊拴在其中的一棵树上.为了使羊在草地上活动区域的面积最大,应将绳子拴在( )
如图,边长为12米的正方形池塘的周围是草地,池塘边A、B、C、D处各有一棵树,且AB=BC=CD=3米.现用长4米的绳子将一头羊拴在其中的一棵树上.为了使羊在草地上活动区域的面积最大,应将绳子拴在( )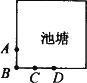
 如图,边长为12米的正方形池塘的周围是草地,池塘边A、B、C、D处各有一棵树,且AB=BC=CD=3米.现用长4米的绳子将一头羊拴在其中的一棵树上.为了使羊在草地上活动区域的面积最大,应将绳子拴在
如图,边长为12米的正方形池塘的周围是草地,池塘边A、B、C、D处各有一棵树,且AB=BC=CD=3米.现用长4米的绳子将一头羊拴在其中的一棵树上.为了使羊在草地上活动区域的面积最大,应将绳子拴在