题目内容
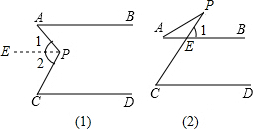
小题1:分别探讨下面两个图形中∠APC与∠A、∠C的数量关系;
小题2:请你从所得到的关系中任选一个加以证明.


小题1:如图(1):∠APC=∠A+∠C,…………2分
如图(2):∠C=∠A+∠APC;…………4分
小题2:图(1):∠APC=∠A+∠C,
过点P作PE∥AB,
∵AB∥CD,
∴AB∥CD∥PE,
∴∠1=∠A,∠2=∠C,
∴∠APC=∠1+∠2=∠A+∠C;
图(2):∠C=∠APC+∠A,
∵AB∥CD,
∴∠1=∠C,
∵∠1=∠A+∠APC,
∴∠C=∠A+∠APC.………………10分
图(1)首先过点P作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,内错角相等,即可求得答案;图(2)由AB∥CD,根据两直线平行,同位角相等,即可求得∠1=∠C,又由三角形外角的性质,即可求得答案;


练习册系列答案
相关题目
 和
和 是同位角的是( )
是同位角的是( )

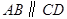 ,能得到
,能得到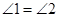 的是
的是
 是
是 的角平分线,
的角平分线, ∥
∥ ,如果
,如果 ,那么
,那么 °.
°.