题目内容
（2004•聊城）如图，矩形ABCD中，AB=6，BC=4．（1）画出以矩形的两条对称轴为坐标轴（x轴平行于AB）的平面直角坐标系，并写出点A，BC的中点E，DC的中点F的坐标；
（2）求过点A，E，F三点的抛物线的解析式，并写出此抛物线的顶点坐标．
【答案】分析：（1）根据矩形的对称性可知：E、F分别在x轴和y轴上，因此E（3，0），F（0，2）；由于DF=
CD=3，BE=
BC=2，因此A（-3，-2）．
（2）可根据（1）题得出的A、E、F三点坐标，用待定系数法可求出抛物线的解析式．进而可用配方法或公式法求出抛物线顶点坐标．
解答：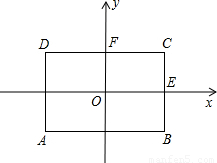
解：（1）A（-3，-2），E（3，0），F（0，2）．
（2）易知：A（-3，-2）．
设抛物线的解析式为y=ax2+bx+c，由于抛物线过A、E、F三点，则有：
，
解得
，
∴抛物线y=-
x2+
x+2，顶点（
）．
点评：本题考查了建立平面直角坐标系的能力以及二次函数解析式的确定等知识．
CD=3，BE=BC=2，因此A（-3，-2）．（2）可根据（1）题得出的A、E、F三点坐标，用待定系数法可求出抛物线的解析式．进而可用配方法或公式法求出抛物线顶点坐标．
解答：
解：（1）A（-3，-2），E（3，0），F（0，2）．（2）易知：A（-3，-2）．
设抛物线的解析式为y=ax2+bx+c，由于抛物线过A、E、F三点，则有：
，解得
，∴抛物线y=-
x2+x+2，顶点（）．点评：本题考查了建立平面直角坐标系的能力以及二次函数解析式的确定等知识．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
