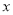题目内容
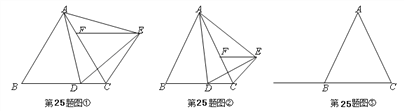
【题目】如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC.
(1)求证:AE是∠DAB的平分线;
(2)探究:线段AD、AB、CD之间有何数量关系?请证明你的结论.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)作EF⊥AD于F,由角平分线的性质就可以得出EF=EC,就可以得出EF=EB,由∠B=90°就可以得出结论;
(2)先由△DEC≌△DEF得出EC=EF,再由△AEB≌△AEF就可以得出AB=AF进而就可以得出AD=AB+CD.
解:(1)作EF⊥AD于F,
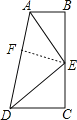
∴∠DFE=∠AFE=90°.
∵∠B=∠C=90°,
∴∠B=∠AFE=∠DFE=∠C=90°.
∴CB⊥AB,CB⊥CD.
∵DE平分∠ADC.
∴∠EDC=∠EDF,CE=CF.
∵E是BC的中点,
∴CE=BE,
∴BE=EF.
在Rt△AEB和Rt△AEF中,![]()
∴Rt△AEB≌Rt△AEF(HL),
∴∠EAB=∠EAF,
∴AE是∠DAB的平分线;
(2)在△DEC和△DEF中, 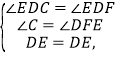
∴△DEC≌△DEF(AAS),
∴CD=FD.EC=EF.
∴在Rt△AEB和Rt△AEF中,![]() ,
,
∴Rt△AEB≌Rt△AEF(HL),
∴AB=AF.
∵AD=AF+DF,
∴AD=AB+CD.

练习册系列答案
相关题目