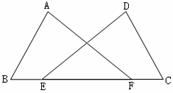
题目内容
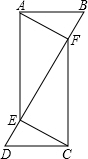 如图点E、F在线段BD上,AB=CD,∠B=∠D,BF=DE.求证:
如图点E、F在线段BD上,AB=CD,∠B=∠D,BF=DE.求证:(1)AE=CF.
(2)AE∥CF.
(3)∠AFE=∠CEF.
分析:(1)先证明△ABF≌△DCE就可以得出AF=CE,∠1=∠2,就可以得出∠3=∠4,即∠AFE=∠CEF;
(2)通过条件证明△AFE≌△CEF就可以得出AEAE=CFCF;
(3)由△AFE≌△CEF,就可以得出∠5=∠6,就有AE∥CF.
(2)通过条件证明△AFE≌△CEF就可以得出AEAE=CFCF;
(3)由△AFE≌△CEF,就可以得出∠5=∠6,就有AE∥CF.
解答:证明:(3)在△ABF和△DCE中,
,
∴△ABF≌△DCE(SAS)
∴AF=CE,∠1=∠2
∵∠1+∠3=180°,∠2+∠4=180°,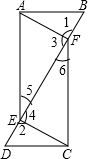
∴∠3=∠4.
即∠AFE=∠CEF;
(1)在△AFE和△CEF中,
,
∴△AFE≌△CEF(SAS)
∴AE=CF;
(2)∵△AFE≌△CEF
∴∠5=∠6
∴AE∥CF.
|
∴△ABF≌△DCE(SAS)
∴AF=CE,∠1=∠2
∵∠1+∠3=180°,∠2+∠4=180°,

∴∠3=∠4.
即∠AFE=∠CEF;
(1)在△AFE和△CEF中,
|
∴△AFE≌△CEF(SAS)
∴AE=CF;
(2)∵△AFE≌△CEF
∴∠5=∠6
∴AE∥CF.
点评:本题考查了等角的补角相等的性质的运用,全等三角形的判定与性质的运用,解答时证明三角形全等是关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
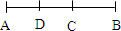 8、如图点C、D在线段AB上,BC=4cm,BD=7cm,且D是线段AC的中点,则AB=
8、如图点C、D在线段AB上,BC=4cm,BD=7cm,且D是线段AC的中点,则AB=
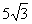 D.10
D.10