题目内容
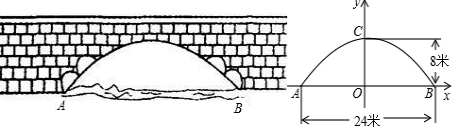
如图所示，在离水面高度5米的岸上有人用绳子拉船靠岸，开始时绳子BC的长度为13米，此人以每秒0.5米的速度收绳．问：（1）未开始收绳的时候，图中船B距岸A的长度AB是多少米？
（2）收绳10秒后船向岸边移动了多少米？（结果保留根号）
分析：（1）在Rt△ABC中，利用勾股定理求得线段AB的长即可
（2）在Rt△ADC中，利用勾股定理求得线段AD的长后即可求得线段BD的长．
（2）在Rt△ADC中，利用勾股定理求得线段AD的长后即可求得线段BD的长．
解答：
解：（1）在Rt△ABC中，
AB=
=
=12米，
所以船B距岸A的长度AB是12米．
（2）设10秒后船移动到点D，在Rt△ADC中，
CD=13-10×0.5=8米，
AD=
=
=
米，
BD=AB-AD=（12-
）米，
所以，收绳10秒船向岸边移动了=（12-
）米．
解：（1）在Rt△ABC中，AB=
| BC2-AC2 |
| 132-52 |
所以船B距岸A的长度AB是12米．
（2）设10秒后船移动到点D，在Rt△ADC中，
CD=13-10×0.5=8米，
AD=
| CD2-AC2 |
| 82-52 |
| 39 |
BD=AB-AD=（12-
| 39 |
所以，收绳10秒船向岸边移动了=（12-
| 39 |
点评：本题考查勾股定理的应用，解题的关键是从几何图形中整理出直角三角形并利用勾股定理正确的求解．
练习册系列答案
相关题目
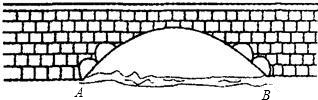
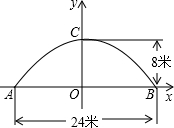
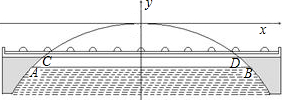
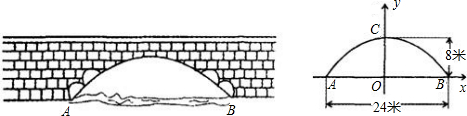
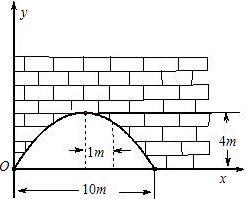有一个抛物线形的拱形桥洞，桥面离水面的距离为5.6米，桥洞离水面的最大高度为4m，跨度为10m，如图所示，把它的图形放在直角坐标系中．
