题目内容
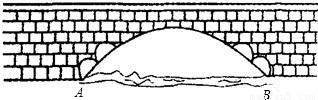
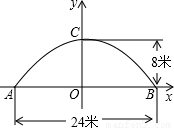
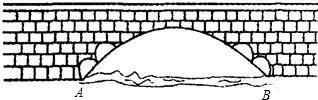
如图所示是永州八景之一的愚溪桥,桥身横跨愚溪,面临潇水,桥下冬暖夏凉,常有渔船停泊桥下避晒纳凉.已知主桥拱为抛物线型,在正常水位下测得主拱宽24m,最高点离水面8m,以水平线AB为x轴,24m的中点为原点建立坐标系.①求此桥拱线所在抛物线的解析式;
②桥边有一浮在水面部分高4m,最宽处12
| 2 |
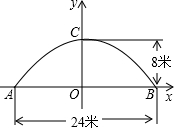
分析:(1)如图可求出A、B、C的坐标,代入函数关系式可得a,b,c的值.
(2)当y=4时求出x的值即可求解.
(2)当y=4时求出x的值即可求解.
解答:解:(1)设抛物线为y=ax2+bx+c
由题意得:A(-12,0),B(12,0),C(0,8).
C点坐标代入得:c=8(2分)
A,B点坐标代入得:
(4分)
解得
,
所求抛物线为y=-
x2+8(6分)
(2)能开到桥下,
理由:当y=4时得
=4,解得:x=±6
(8分)
高出水面4m处,拱宽12
m=12
m(船宽)
所以此船在正常水位时可以开到桥下.(10分)
由题意得:A(-12,0),B(12,0),C(0,8).
C点坐标代入得:c=8(2分)
A,B点坐标代入得:
|
解得
|
所求抛物线为y=-
| 1 |
| 18 |
(2)能开到桥下,
理由:当y=4时得
| x2 |
| 18 |
| 2 |
高出水面4m处,拱宽12
| 2 |
| 2 |
所以此船在正常水位时可以开到桥下.(10分)
点评:(1)用待定系数法求解析式的步骤为:①设出所求函数的解析式;②根据已知条件,列出方程组;③解方程组,求出待定系数;④下结论(2)无论是求解析式或运用其解析式解决有关问题,都需要根据问题的条件,选取恰当的形式

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

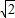 m的河鱼餐船,试探索此船能否开到桥下?说明理由.
m的河鱼餐船,试探索此船能否开到桥下?说明理由.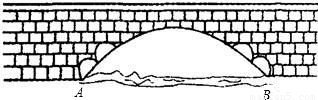
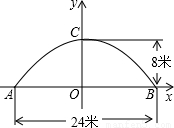

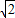 m的河鱼餐船,试探索此船能否开到桥下?说明理由.
m的河鱼餐船,试探索此船能否开到桥下?说明理由.