题目内容
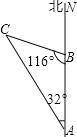
【题目】上午8时,一条船从A处出发以30海里/时的速度向正北航行,12时到达B处.测得∠NAC=32°,∠ABC=116°.求从B处到灯塔C的距离?
【答案】120海里
【解析】
试题分析:根据已知条件“上午8时,一条船从A处出发以30海里/时的速度向正北航行,12时到达B处”可以求得AB=120海里,然后根据三角形的内角和定理求得∠C=32°,所以△ABC是等腰三角形;最后由等腰三角形的两腰相等的性质来求从B处到灯塔C的距离.
解:根据题意,得
AB=30×4=120(海里);
在△ABC中,∠NAC=32°,∠ABC=116°,
∴∠C=180°﹣∠NAC﹣∠ABC=32°,
∴∠C=∠NAC,
∴BC=AB=120(海里),
即从B处到灯塔C的距离是120海里.

练习册系列答案
相关题目