Question

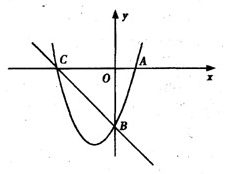
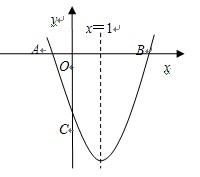
如图，已知抛物线y＝ax²＋bx＋c(a≠0)的对称轴为x＝1，且抛物线经过A（—1，0）、C（0，—3）两点，与x轴交于另一点B．

（1）求这条抛物线所对应的函数关系式；

（2）在抛物线的对称轴x＝1上求一点M，使点M到点A的距离与到点C的距离之和最小，并求出此时点M的坐标；

（3）设点P为抛物线的对称轴x＝1上的一动点，求使∠PCB＝90°的点P的坐标．

Answer 1

（1）设抛物线的解析式为y ＝ax²＋bx＋c，则有：

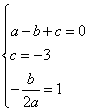解得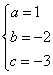：，所以抛物线的解析式为y ＝x²－2x－3．

（2）令x²－2x－3＝0，解得x₁＝－１，x₂＝3,所以B点坐标为（3，0）．

设直线BC的解析式为y ＝kx＋b,

则，解得，所以直线解析式是y ＝x－3．

当x＝1时，y＝－2．所以M点的坐标为（1，－2）．

（3）方法一：要使∠PBC＝90°，则直线PC过点C，且与BC垂直，

又直线BC的解析式为y ＝x－3，

所以直线PC的解析式为y ＝－x－3，当x＝1时，y＝－4，

所以P点坐标为（1，－4）．

方法二：设P点坐标为（1，y），则PC²＝1²＋（－3－y）²,

BC²＝3²＋3²；PB²＝2²＋y²

由∠PBC＝90°可知△PBC是直角三角形，且PB为斜边，则有PC²＋BC²＝PB²．

所以：[1²＋（－3－y）²]＋[3²＋3²]＝2²＋y²；解得y ＝－4，

所以P点坐标为（1，－4）．