题目内容
 (1)阅读下面材料:
(1)阅读下面材料:点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为AB.
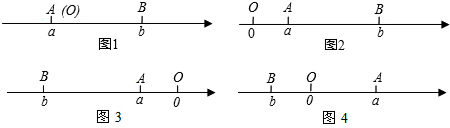
当A、B两点中有一点在原点时,不妨设点A在原点,
如图甲,AB=OB=|b|=|a-b|;
当A、B两点都不在原点时,
1 如图乙,点A、B都在原点的右边,
AB=OB-OA=|b|-|a|=b-a=|a-b|;
②如图丙,点A、B都在原点的左边,
AB=OB-OA=|b|-|a|=-b-(-a)=|a-b|;
③如图丁,点A、B在原点的两边
AB=OA+OB=|a|+|b|=a+(-b)=|a-b|.
综上,数轴上A、B两点之间的距离AB=|a-b|.
(2)回答下列问题:
①数轴上表示2和5的两点之间的距离是
3
3
,数轴上表示-2和-5的两点之间的距离是3
3
,数轴上表示1和-3的两点之间的距离是4
4
;②数轴上表示x和-1的两点分别是点A和B,则A、B之间的距离是
|x+1|
|x+1|
,如果|AB|=2,那么x=1或3
1或3
;③当代数式|x+2|+|x-5|取最小值时,相应的x的取值范围是
7
7
.④当代数式|x-1|+|x+2|+|x-5|取最小值时,相应的x的值是
7
7
.⑤当代数式|x-5|-|x+2|取最大值时,相应的x的取值范围是
7
7
.分析:①、根据(1)中的知识可以得到两点之间的距离就是较大的数与较小的数的差,据此即可求解;
②、根据(1),即可直接写出结果;
③、|x+2|+|x-5|表示数轴上一点到-2与5两点的距离的和,当这点是-2或5,以及它们之间时和最小,最小距离是-2与5之间的距离;
④、代数式|x-1|+|x+2|+|x-5|表示数轴上一点到1、-2与5三点的距离的和,根据两点之间线段最短,则当x=1时和最小,最小值是5到-2的距离;
⑤、代数式|x-5|-|x+2|表示数轴上一点到5与-2两点的距离的差,当点不在-2与5之间时差最大,最大值是5与-2之间的距离.
②、根据(1),即可直接写出结果;
③、|x+2|+|x-5|表示数轴上一点到-2与5两点的距离的和,当这点是-2或5,以及它们之间时和最小,最小距离是-2与5之间的距离;
④、代数式|x-1|+|x+2|+|x-5|表示数轴上一点到1、-2与5三点的距离的和,根据两点之间线段最短,则当x=1时和最小,最小值是5到-2的距离;
⑤、代数式|x-5|-|x+2|表示数轴上一点到5与-2两点的距离的差,当点不在-2与5之间时差最大,最大值是5与-2之间的距离.
解答:解:①.5-2=3,-2-(-5)=3,1-(-3)=4;
②、|x+1|,|x+1|=2则x=1或-3;
③|x+2|+|x-5|表示数轴上一点到-2与5两点的距离的和,当这点在-2和5之间时和最小,最小距离是:5-(-2)=7;
④代数式|x-1|+|x+2|+|x-5|表示数轴上一点到1、-2与5三点的距离的和,根据两点之间线段最短,则当x=1时和最小,最小值是5到-2的距离,是5-(-2)=7;
⑤代数式|x-5|-|x+2|表示数轴上一点到5与-2两点的距离的差,当点不在-2与5之间时差最大,最大值是5与-2之间的距离,是7.
故答案是:①3,3,4;
②|x+1|,1或3;
③7;
④7;
⑤7.
②、|x+1|,|x+1|=2则x=1或-3;
③|x+2|+|x-5|表示数轴上一点到-2与5两点的距离的和,当这点在-2和5之间时和最小,最小距离是:5-(-2)=7;
④代数式|x-1|+|x+2|+|x-5|表示数轴上一点到1、-2与5三点的距离的和,根据两点之间线段最短,则当x=1时和最小,最小值是5到-2的距离,是5-(-2)=7;
⑤代数式|x-5|-|x+2|表示数轴上一点到5与-2两点的距离的差,当点不在-2与5之间时差最大,最大值是5与-2之间的距离,是7.
故答案是:①3,3,4;
②|x+1|,1或3;
③7;
④7;
⑤7.
点评:本题考查了数轴,用几何方法借助数轴来求解,非常直观,体现了数形结合的优点.

练习册系列答案
相关题目
阅读下面材料:
在计算1+4+7+10+13+16+19+22+25+28时,我们发现,从第一个数开始,以后的每个数与它的前一个数的差都是一个相同的定值,具有这种规律的一列数,求和时,除了直接相加外,我们还可以用公式S=na+
×d来计算(公式中的S表示它们的和,n表示数的个数,a表示第一个数的值,d表示这个相差的定值).那么S=1+4+7+10+13+16+19+22+25+28=10×1+
×3=145.
用上面的知识解决下列问题:
我市某乡镇具有“中国北方乔木之乡”的美称,到2000年底这个镇已有苗木2万亩,为增加农民收入,这个镇实施“苗木兴镇”战略,逐年有计划地扩种苗木.从2001年起,以后每年又比上一年多种植相同面积的苗木;从2001年起每年卖出成苗木,以后每年又比上一年多卖出相同面积的苗木.下表为2001年、2002年、2003年三年种植苗木与卖出成苗木的面积统计数据.
假设所有苗木的成活率都是100%,问到哪一年年底,这个镇的苗木面积达到5万亩?
在计算1+4+7+10+13+16+19+22+25+28时,我们发现,从第一个数开始,以后的每个数与它的前一个数的差都是一个相同的定值,具有这种规律的一列数,求和时,除了直接相加外,我们还可以用公式S=na+
| n(n-1) |
| 2 |
| 10(10-1) |
| 2 |
用上面的知识解决下列问题:
我市某乡镇具有“中国北方乔木之乡”的美称,到2000年底这个镇已有苗木2万亩,为增加农民收入,这个镇实施“苗木兴镇”战略,逐年有计划地扩种苗木.从2001年起,以后每年又比上一年多种植相同面积的苗木;从2001年起每年卖出成苗木,以后每年又比上一年多卖出相同面积的苗木.下表为2001年、2002年、2003年三年种植苗木与卖出成苗木的面积统计数据.
| 年份 | 2001年 | 2002年 | 2003年 |
| 每年种植苗木的面积(亩) | 4000 | 5000 | 6000 |
| 每年卖出成苗木的面积(亩) | 2000 | 2500 | 3000 |