题目内容
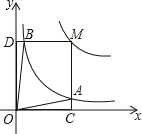
【题目】如图,⊙O是△ACD的外接圆,AB是直径,过点D作直线DE∥AB,过点B作直线BE∥AD,两直线交于点E,如果∠ACD=45°,⊙O的半径是4cm
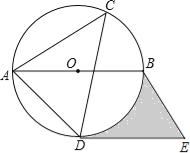
(1)请判断DE与⊙O的位置关系,并说明理由;
(2)求图中阴影部分的面积(结果用π表示).
【答案】(1)DE与⊙O相切,证明见解析;(2)(24-4π)cm2.
【解析】
(1)连接OD,根据圆周角定理得∠ABD=∠ACD=45°,∠ADB=90°,可判断△ADB为等腰直角三角形,所以OD⊥AB,而DE∥AB,则有OD⊥DE,然后根据切线的判定定理得到DE为⊙O的切线.
(2)由BE∥AD,DE∥AB得到四边形ABED为平行四边形,则DE=AB=8cm,然后根据梯形的面积公式和扇形的面积公式,利用S阴影部分=S梯形BODE﹣S扇形OBD求得图中阴影部分的面积.
解:(1)DE与⊙O相切.理由如下:
连接OD,BD,
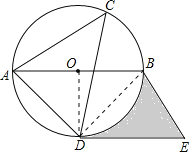
∵AB是直径,
∴∠ADB=90°.
∴∠ABD=∠ACD=45°.
∴△ADB为等腰直角三角形.
∵点O为AB的中点,
∴OD⊥AB.
∵DE∥AB,
∴OD⊥DE.
∴DE为⊙O的切线.
(2)∵BE∥AD,DE∥AB,
∴四边形ABED为平行四边形.
∴DE=AB=8cm.
![]()
![]() ,
,
=(24-4π)cm2.

练习册系列答案
相关题目