题目内容
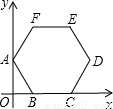
 如图,半径长为2的正六边形ABCDEF的顶点A在y轴上,边BC在x轴上,则点E的坐标是
如图,半径长为2的正六边形ABCDEF的顶点A在y轴上,边BC在x轴上,则点E的坐标是(3,2
)
| 3 |
(3,2
)
.| 3 |
分析:首先取正六边形ABCDEF的中心G,连接AG,DG,FG,EG,EC,可得△AFG,△EGF,△DGE是等边三角形,然后由等边三角形的性质,即可求得AH与EH的长,继而求得答案.
解答: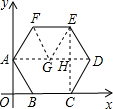 解:取正六边形ABCDEF的中心G,连接AG,DG,FG,EG,EC,
解:取正六边形ABCDEF的中心G,连接AG,DG,FG,EG,EC,
∴∠AGF=∠EGF=∠EGD=60°,
∴A,G,D共线,
∵AG=FG=EG=GD,
∴△AFG,△EGF,△DGE是等边三角形,
∵半径长为2的正六边形ABCDEF的顶点A在y轴上,
∴AG=EG=ED=GD=2,
∵AD⊥EC,
∴GH=
GD=1,
∴AH=3,
即OC=3,
∵EH=
=
,
∴EC=2
,
∴点E的坐标是:(3,2
).
故答案为:(3,2
).
 解:取正六边形ABCDEF的中心G,连接AG,DG,FG,EG,EC,
解:取正六边形ABCDEF的中心G,连接AG,DG,FG,EG,EC,∴∠AGF=∠EGF=∠EGD=60°,
∴A,G,D共线,
∵AG=FG=EG=GD,
∴△AFG,△EGF,△DGE是等边三角形,
∵半径长为2的正六边形ABCDEF的顶点A在y轴上,
∴AG=EG=ED=GD=2,
∵AD⊥EC,
∴GH=
| 1 |
| 2 |
∴AH=3,
即OC=3,
∵EH=
| EG2-GH2 |
| 3 |
∴EC=2
| 3 |
∴点E的坐标是:(3,2
| 3 |
故答案为:(3,2
| 3 |
点评:此题考查了正多边形与圆的知识.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
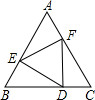 如图,边长为n的正△DEF的三个顶点恰好在边长为m的正△ABC的各边上,则△AEF的内切圆半径为( )
如图,边长为n的正△DEF的三个顶点恰好在边长为m的正△ABC的各边上,则△AEF的内切圆半径为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
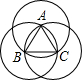 如图,边长为1的正△ABC,分别以顶点A,B,C为圆心,1为半径作圆,那么这三个圆所覆盖的图形面积为
如图,边长为1的正△ABC,分别以顶点A,B,C为圆心,1为半径作圆,那么这三个圆所覆盖的图形面积为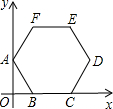 如图,半径长为2的正六边形ABCDEF的顶点A在y轴上,边BC在x轴上,则点E的坐标是________.
如图,半径长为2的正六边形ABCDEF的顶点A在y轴上,边BC在x轴上,则点E的坐标是________.