题目内容
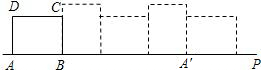已知矩形ABCD的长AB=4，宽AD=3，按如图放置在直线AP上，然后不滑动，只转动，当它转动A→A′时，顶点A所经过的路线长等于多少？分析：矩形ABCD在直线AP上转动一周，顶点A经过的路线是三段弧，这三段弧的圆心角都是90°，半径分别是4，5和3，利用弧长公式计算求出点A经过的路线长．
解答：解：L=L1+L2+L3=
п×4+
п×5+
п×3=6п．
答：当它转动A→A′时，顶点A所经过的路线长等于6π．
| 90 |
| 180 |
| 90 |
| 180 |
| 90 |
| 180 |
答：当它转动A→A′时，顶点A所经过的路线长等于6π．
点评：本题考查的是弧长的计算，分析题意得到点A经过的路线是三段弧，并且知道弧的半径和圆心角，利用弧长公式计算求出这三段弧长，它们的和就是点A经过的路线的长．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
点O在矩形ABCD内可随意运动，已知矩形ABCD的长为4，宽为3，则O到点A的距离不超过1的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、1-
|
