题目内容
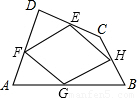
 如图,顺次连接△ABC各边中点D,E,F,则图中共有_____个平行四边形.
如图,顺次连接△ABC各边中点D,E,F,则图中共有_____个平行四边形.
- A.1
- B.2
- C.3
- D.4
C
分析:由于点D,E,F分别是各边的中点,所以易证DE、DF、EF是三角形的中位线,所以图中的平行四边形有:?AEFD、?BEDF、?EFDC.
解答:∵D,E,F是△ABC各边中点
∴DE= BC,DE∥BC
BC,DE∥BC
而BF=FC
∴DE=FC且DE∥FC
∴DEFC为平行四边形
同理可证:四边形DEBF、ADEF为平行四边形
∴共有3个平行四边形
故选C.
点评:本题考查了平行四边形的判定和三角形的中位线定理,三角形的中位线的性质定理,为题目提供了平行线,为利用平行线判定平行四边形奠定了基础.
分析:由于点D,E,F分别是各边的中点,所以易证DE、DF、EF是三角形的中位线,所以图中的平行四边形有:?AEFD、?BEDF、?EFDC.
解答:∵D,E,F是△ABC各边中点
∴DE=
 BC,DE∥BC
BC,DE∥BC而BF=FC
∴DE=FC且DE∥FC
∴DEFC为平行四边形
同理可证:四边形DEBF、ADEF为平行四边形
∴共有3个平行四边形
故选C.
点评:本题考查了平行四边形的判定和三角形的中位线定理,三角形的中位线的性质定理,为题目提供了平行线,为利用平行线判定平行四边形奠定了基础.

练习册系列答案
相关题目
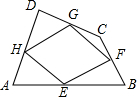 如图,顺次连接四边形ABCD各中点得四边形EFGH,要使四边形EFGH为菱形,应添加的条件是( )
如图,顺次连接四边形ABCD各中点得四边形EFGH,要使四边形EFGH为菱形,应添加的条件是( )| A、AB∥DC | B、AB=DC | C、AC⊥BD | D、AC=BD |
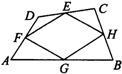 5、如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是( )
5、如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是( ) 7、如图,顺次连接四边形AB的各边的中点,得到四边形EFGH,在下列条件中,可使四边形EFGH为矩形的是( )
7、如图,顺次连接四边形AB的各边的中点,得到四边形EFGH,在下列条件中,可使四边形EFGH为矩形的是( )