题目内容
14、在一张长为9cm,宽为8cm的矩形纸片上裁取一个与该矩形三边都相切的圆片后,余下的部分中能裁取的最大圆片的半径为
1
cm.分析:根据题意知:裁去的与三边都相切的圆的半径应该是4cm;余下的要截取的最大圆,应和矩形的两邻边以及裁去的圆都相切,然后可通过构建直角三角形求解.
解答: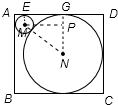 解:如图;四边形ABCD是矩形,AB=8cm,AD=9cm;
解:如图;四边形ABCD是矩形,AB=8cm,AD=9cm;
由题意,知:⊙N的半径为4cm,即NG=4cm;
设小圆的半径为r,则:
MN=4+r,NP=4-r,MP=AG-AE=5-r;
Rt△NPM中,由勾股定理,得:
MN2=NP2+MP2,即:
(4+r)2=(4-r)2+(5-r)2,
解得:r=1或25(不符合题意,应舍去).
故余下的部分中,能裁取的最大圆片的半径为1cm.
 解:如图;四边形ABCD是矩形,AB=8cm,AD=9cm;
解:如图;四边形ABCD是矩形,AB=8cm,AD=9cm;由题意,知:⊙N的半径为4cm,即NG=4cm;
设小圆的半径为r,则:
MN=4+r,NP=4-r,MP=AG-AE=5-r;
Rt△NPM中,由勾股定理,得:
MN2=NP2+MP2,即:
(4+r)2=(4-r)2+(5-r)2,
解得:r=1或25(不符合题意,应舍去).
故余下的部分中,能裁取的最大圆片的半径为1cm.
点评:此题首先要画出正确的图形,然后根据两圆的位置关系及勾股定理列方程计算.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 28、如图所示,在一张长为9cm,宽为8cm的矩形纸片上,截取一个与该矩形三边都相切的圆片后,求余下的部分中能截取的最大圆片的半径是多少?
28、如图所示,在一张长为9cm,宽为8cm的矩形纸片上,截取一个与该矩形三边都相切的圆片后,求余下的部分中能截取的最大圆片的半径是多少?
