题目内容
判断下列各题是否正确?
(1)不等式两边同时乘以一个整数,不等号方向不变.______
(2)如果a>b,那么3-2a>3-2b.______
(3)如果a是有理数,那么-8a>-5a.______
(4)如果a<b,那么a2<b2.______
(5)如果a为有理数,则a>-a.______
(6)如果a>b,那么ac2>bc2.______
(7)如果-x>8,那么x>-8.______
(8)若a<b,则a+c<b+c.______
解:(1)×,注意当此整数为0时,此不等式变为等式了,当此整数为负数时,不等号应改变方向;
(2)×,正确答案应为3-2a<3-2b,这可由不等式的基本性质3得到;
(3)×,当a<0时,-8a<-5a;
(4)×,当a=-4,b=1时,有a<b,但a2>b2;
(5)×,当a≤0时,a≤-a;
(6)×,当c=0时,ac2=bc2;
(7)×,由不等式的基本性质3应有x<-8;
(8)√,这可由不等式的基本性质1得到.
分析:(1)利用不等式性质(2),应该是同乘以一个正数,不等号方向不变,故错误;(2)先利用不等式性质(3),同乘以-2,不等号方向改变,再利用不等式性质(1),同加上3,不等号方向不变,故错误;(3)若a<0,利用不等式性质(3),在-8<-5的基础上,可知-8a>-5a,故错误;(4)可以举出反例,如a=-4,b=1,a<b,但是a2>b2,故错误;(5)若a<0,则-a>0,故a<-a,故错误;(6)若c=0,同乘以0,就是等式了,故错误;(7)利用不等式性质(3),同乘以-1,不等号改变,则x<-8,故错误;(8)利用不等式性质(1),同加上c,不等号方向不变,有a+c<b+c,故正确.
点评:不等式的性质:
(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.
(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.
(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.
(2)×,正确答案应为3-2a<3-2b,这可由不等式的基本性质3得到;
(3)×,当a<0时,-8a<-5a;
(4)×,当a=-4,b=1时,有a<b,但a2>b2;
(5)×,当a≤0时,a≤-a;
(6)×,当c=0时,ac2=bc2;
(7)×,由不等式的基本性质3应有x<-8;
(8)√,这可由不等式的基本性质1得到.
分析:(1)利用不等式性质(2),应该是同乘以一个正数,不等号方向不变,故错误;(2)先利用不等式性质(3),同乘以-2,不等号方向改变,再利用不等式性质(1),同加上3,不等号方向不变,故错误;(3)若a<0,利用不等式性质(3),在-8<-5的基础上,可知-8a>-5a,故错误;(4)可以举出反例,如a=-4,b=1,a<b,但是a2>b2,故错误;(5)若a<0,则-a>0,故a<-a,故错误;(6)若c=0,同乘以0,就是等式了,故错误;(7)利用不等式性质(3),同乘以-1,不等号改变,则x<-8,故错误;(8)利用不等式性质(1),同加上c,不等号方向不变,有a+c<b+c,故正确.
点评:不等式的性质:
(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.
(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.
(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
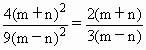 ( );
( );