题目内容
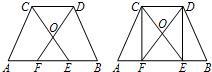22、如图①，在等腰梯形ABCD中，AB∥CD，E、F是边AB上的两点，且AE=BF，DE与CF相交于梯形ABCD内一点O．（1）求证：OE=OF；
（2）如图②，当EF=CD时，请你连接DF、CE，判断四边形DCEF是什么样的四边形，并证明你的结论．
分析：（1）由等腰梯形的性质得AD=BC，∠A=∠B，因为AE=BF，根据SAS判定△ACE≌△BDF，从而得到∠CEA=∠DFB，即OE=OF；
（2）根据一组对边平行且相等的四边形是平行四边形，得到四边形DCEF是平行四边形，又知CE=DF，所以得到四边形DCEF是矩形．
（2）根据一组对边平行且相等的四边形是平行四边形，得到四边形DCEF是平行四边形，又知CE=DF，所以得到四边形DCEF是矩形．
解答：证明：（1）∵梯形ABCD为等腰梯形，AB∥CD
∴AC=BD，∠A=∠B
∵AE=BF
∴△ACE≌△BDF
∴∠CEA=∠DFB
∴OE=OF；
（2）∵DC∥EF且DC=EF
∴四边形CDEF是平行四边形
又由（1）得△ACE≌△BDF
∴CE=DF，
∴?CDEF为矩形．
∴AC=BD，∠A=∠B
∵AE=BF
∴△ACE≌△BDF
∴∠CEA=∠DFB
∴OE=OF；
（2）∵DC∥EF且DC=EF
∴四边形CDEF是平行四边形
又由（1）得△ACE≌△BDF
∴CE=DF，
∴?CDEF为矩形．
点评：此题主要考查学生对等腰梯形的性质，全等三角形的判定及矩形的判定的理解及运用．
练习册系列答案
名校课堂系列答案
相关题目
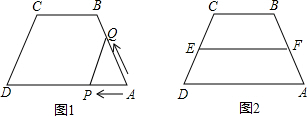条件时，其一定平分梯形的面积？（只要求说出条件，不需证明）
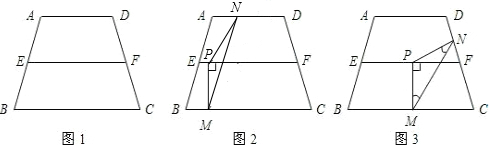
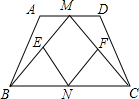（2009•黔南州）杨老师在上四边形时给学生出了这样一个题．如图，若在等腰梯形ABCD中，M、N分别是AD、BC的中点，E、F分别是BM、CM的中点时．提出以下问题：