题目内容
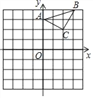
【题目】已知有理数a，b在数轴上的位置如图所示．
（1）在数轴上标出﹣a，﹣b的位置，并比较a，b，﹣a，﹣b的大小：
（2）化简|a+b|+|a﹣b|．
【答案】（1）图见解析，b＜﹣a＜a＜﹣b；（2）﹣2b.
【解析】
试题（1）首先根据-a与a，-b与b互为相反数，-a与a，-b与b表示的点关于原点对称，在数轴上标出-a，-b的位置；然后根据数轴的特征：一般来说，当数轴方向朝右时，右边的数总比左边的数大，比较a，b，-a，-b的大小即可．
（2）根据有理数a，b在数轴上的位置，可得a＞0＞b，而且|a|＜|b|，所以a+b＜0，a-b＞0，据此化简|a+b|+|a-b|即可．
试题解析：（1）如图所示：
，
b＜﹣a＜a＜﹣b．
（2）∵a＞0＞b，而且|a|＜|b|，
∴a+b＜0，a﹣b＞0，
∴|a+b|+|a﹣b|
=﹣（a+b）+（a﹣b）
=﹣a﹣b+a﹣b
=﹣2b
练习册系列答案
名校课堂系列答案
相关题目
