题目内容
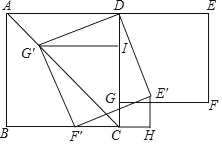
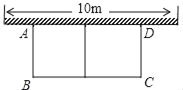
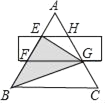
【题目】如图,等边△ABC被一个平行于BC的矩形所截,AB被截成三等份.若BC=a,则图中阴影部分的面积是_____.
【答案】![]()
【解析】
先由等边△ABC被一个平行于BC的矩形所截,AB被截成三等份,可得EH∥BC,那么△AEH∽△ABC,根据相似三角形面积比等于相似比的平方,得出S△AEH=![]() S△ABC,那么S梯形EBCH=
S△ABC,那么S梯形EBCH=![]() S△ABC.再证明FG是梯形EBCH的中位线,EH+BC=2FG.进而得到S△EBG=
S△ABC.再证明FG是梯形EBCH的中位线,EH+BC=2FG.进而得到S△EBG=![]() S梯形EBCH,从而求解即可.
S梯形EBCH,从而求解即可.
解:∵等边△ABC被一个平行于BC的矩形所截,AB被截成三等份,
∴AE=EF=FB=![]() AB=
AB=![]() BC=
BC=![]() a,EH∥BC,
a,EH∥BC,
∴△AEH∽△ABC,
∴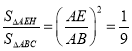 ,
,
∴S△AEH=![]() S△ABC,
S△ABC,
∴S梯形EBCH=S△ABC﹣S△AEH=![]() S△ABC.
S△ABC.
∵EH∥FG∥BC,EF=FB,
∴FG是梯形EBCH的中位线,
∴EH+BC=2FG.
设△EFG的边FG上的高为h,则△BFG的边FG上的高为h,梯形EBCH的高为2h,
∵S△EBG=S△EFG+S△ABFG
=![]() FGh+
FGh+![]() FGh
FGh
=FGh,
S梯形EBCH=![]() (EH+BC)2h
(EH+BC)2h
=![]() 2FG2h
2FG2h
=2FGh,
∴S△EBG=![]() S梯形EBCH=
S梯形EBCH=![]() ×
×![]()
![]() ×
×![]() a2=
a2=![]() a2.
a2.
故答案为![]() a2.
a2.

练习册系列答案
相关题目
【题目】如表:方程1、方程2、方程3、…是按一定规律排列的一列方程.
序号 | 方程 | 方程的解 | |
1 | x2+x﹣2﹣=0 | x1=﹣2 | x2=1 |
2 | x2+2x﹣8﹣=0 | x1=﹣4 | x2=2 |
3 | x2+3x﹣18=0 | x1= | x2= |
… | … | … | … |
(1)解方程3,并将它的解填在表中的空白处;
(2)请写出这列方程中第10个方程,并用求根公式求其解.
(3)根据表中的规律写出第n个方程和这个方程的解.