题目内容
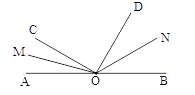
【题目】如图所示,∠AOB是平角,OM、ON分别是∠AOC、∠BOD 的平分线.
(1)知∠AOC=40°,∠BOD=60°,求∠MON的度数;
(2)知∠COD=90°,求出∠MON的度数.
【答案】(1)130°;(2)135°.
【解析】试题分析:(1)根据平角即可求得∠COD的度数,再根据角平分线的定义求得∠COM和∠DON的度数,从而求得∠MON的度数;
(2)因为OM、ON分别是∠AOC、∠BOD的平分线,故知∠MOC+∠NOD=![]() ∠AOC+
∠AOC+![]() ∠BOD=
∠BOD=![]() (∠AOC+∠BOD)即可解答.
(∠AOC+∠BOD)即可解答.
试题解析:(1)∵∠AOB是平角,∠AOC=40°,∠BOD=60°,
∴∠COD=∠A0B-∠AOC-∠BOD=180°-40°-60°=80°,
∵OM、ON分别是∠AOC、∠BOD 的平分线,
![]() ∠COM=
∠COM=![]() ∠AOC=20°,∠DON=
∠AOC=20°,∠DON=![]() ∠BOD=30°,
∠BOD=30°,
![]() ∠MON=∠COM+∠COD+∠DON,
∠MON=∠COM+∠COD+∠DON,
![]() ∠MON=20°+80DU5+30°=130°;
∠MON=20°+80DU5+30°=130°;
(2)![]() ∠COD=90°,
∠COD=90°,
![]() ∠AOC+∠BOD =90°,
∠AOC+∠BOD =90°,
又 ![]() OM、ON分别是∠AOC、∠BOD 的平分线,
OM、ON分别是∠AOC、∠BOD 的平分线,
![]() ∠MOC=
∠MOC=![]() ∠AOC,∠NOD=
∠AOC,∠NOD=![]() ∠BOD,
∠BOD,
即∠MOC+∠NOD=![]() (∠AOC+∠BOD)=45°,
(∠AOC+∠BOD)=45°,
又 ![]() ∠MON=∠MOC+∠NOD+∠COD,
∠MON=∠MOC+∠NOD+∠COD,
![]() ∠MON=45°+90°=135°.
∠MON=45°+90°=135°.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
