题目内容
在直角坐标系xOy 中,已知某二次函数的图象经过A(-4,0)、B(0,-3),与x轴的正半轴相交于点C,若△AOB∽△BOC(相似比不为1).
(1)求这个二次函数的解析式;
(2)求△ABC的外接圆半径r;
(3)在线段AC上是否存在点M(m,0),使得以线段BM为直径的圆与线段AB交于N点,且以点O、A、N为顶点的三角形是等腰三角形?若存在,求出m的值;若不存在,请说明理由.
(1)求这个二次函数的解析式;
(2)求△ABC的外接圆半径r;
(3)在线段AC上是否存在点M(m,0),使得以线段BM为直径的圆与线段AB交于N点,且以点O、A、N为顶点的三角形是等腰三角形?若存在,求出m的值;若不存在,请说明理由.
分析:(1)设二次函数y=ax2+bx+c的解析式,首先求出B点坐标,然后由△AOB∽△BOC,根据相似三角形的对应边成比例,求出OC的长度,得出C点坐标;根据相似三角形的对应角相等得出∠OAB=∠OBC,从而得出∠ABC=90°;由y=ax2+bx+c图象经过点A(-4,0),B(0,-3),运用待定系数法即可求出此二次函数的关系式;
(2)由已知条件证明△ABC是直角三角形,利用直角三角形的外接圆的直径等于其斜边即r=
,求解即可;
(3)如果以点O、A、N为顶点的三角形是等腰三角形,那么分三种情况讨论:①当AN=ON时,②当AN=OA时,当ON=OA时,针对每一种情况,都应首先判断M点是否在线段AC上.
(2)由已知条件证明△ABC是直角三角形,利用直角三角形的外接圆的直径等于其斜边即r=
| c |
| 2 |
(3)如果以点O、A、N为顶点的三角形是等腰三角形,那么分三种情况讨论:①当AN=ON时,②当AN=OA时,当ON=OA时,针对每一种情况,都应首先判断M点是否在线段AC上.
解答:解:(1)∵△AOB∽△BOC(相似比不为1),
∴
=
,
又∵OA=4,OB=3,
∴OC=
=
,
∴点C(
,0),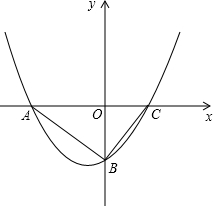
设图象经过A、B、C三点的函数解析式是y=ax2+bx+c,则:
,
解得,a=
,b=
,
∴这个函数的解析式是y=
x2+
x-3;
(2)∵△AOB∽△BOC(相似比不为1),
∴∠BAO=∠CBO.
又∵∠ABO+∠BAO=90°,
∴∠ABC=∠ABO+∠CBO=∠ABO+∠BAO=90°
∴AC是△ABC外接圆的直径.
∴r=
AC=
×(OA+OC)=
;
(3)∵点N在以BM为直径的圆上,
∴∠MNB=90°,
①当AN=ON时,点N在OA的中垂线上,
∴点N1是AB的中点,M1是AC的中点.
∴AM1=r=
,点M1(-
,0),即m1=-
;
②当AN=OA时,Rt△AM2N2≌Rt△ABO,
∴AM2=AB=5,点M2(1,0),即m2=1.
③当ON=OA时,点N显然不能在线段AB上.
综上,符合题意的点M(m,0)存在,有两解:
m=-
,或1.
∴
| OC |
| OB |
| OB |
| OA |
又∵OA=4,OB=3,
∴OC=
| 3×3 |
| 4 |
| 9 |
| 4 |
∴点C(
| 9 |
| 4 |

设图象经过A、B、C三点的函数解析式是y=ax2+bx+c,则:
|
解得,a=
| 1 |
| 3 |
| 7 |
| 12 |
∴这个函数的解析式是y=
| 1 |
| 3 |
| 7 |
| 12 |
(2)∵△AOB∽△BOC(相似比不为1),
∴∠BAO=∠CBO.
又∵∠ABO+∠BAO=90°,
∴∠ABC=∠ABO+∠CBO=∠ABO+∠BAO=90°
∴AC是△ABC外接圆的直径.
∴r=
| 1 |
| 2 |
| 1 |
| 2 |
| 25 |
| 8 |
(3)∵点N在以BM为直径的圆上,
∴∠MNB=90°,
①当AN=ON时,点N在OA的中垂线上,
∴点N1是AB的中点,M1是AC的中点.
∴AM1=r=
| 25 |
| 8 |
| 7 |
| 8 |
| 7 |
| 8 |
②当AN=OA时,Rt△AM2N2≌Rt△ABO,
∴AM2=AB=5,点M2(1,0),即m2=1.
③当ON=OA时,点N显然不能在线段AB上.
综上,符合题意的点M(m,0)存在,有两解:
m=-
| 7 |
| 8 |
点评:本题着重考查了待定系数法求二次函数解析式,相似三角形的性质,探究等腰三角形的构成情况等重要知识点,综合性强,能力要求高.考查学生分类讨论,数形结合的数学思想方法.

练习册系列答案
相关题目
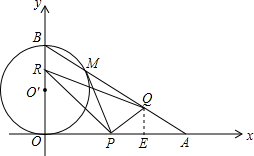 如图,在直角坐标系xoy中,O是坐标原点,点A在x正半轴上,OA=
如图,在直角坐标系xoy中,O是坐标原点,点A在x正半轴上,OA=
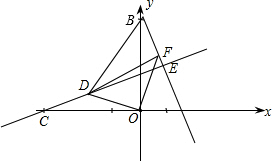
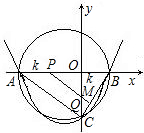 物线的解析式为y=
物线的解析式为y= 在直角坐标系xoy中,一次函数
在直角坐标系xoy中,一次函数