题目内容
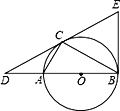
【题目】如图,抛物线y=ax2+bx+c(a≠0)的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,且OD=OC.
(1)求直线CD的解析式;
(2)求抛物线的解析式;
(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,求证:△CEQ∽△CDO;
(4)在(3)的条件下,若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
【答案】解:(1)∵C(0,1),OD=OC,∴D点坐标为(1,0)。
设直线CD的解析式为y=kx+b(k≠0),
将C(0,1),D(1,0)代入得:![]() ,解得:。
,解得:。
∴直线CD的解析式为:y=﹣x+1。
(2)设抛物线的解析式为y=a(x﹣2)2+3,
将C(0,1)代入得:1=a×(﹣2)2+3,解得a=![]() 。
。
∴y=![]() (x﹣2)2+3=
(x﹣2)2+3=![]() x2+2x+1。
x2+2x+1。
(3)证明:由题意可知,∠ECD=45°,
∵OC=OD,且OC⊥OD,∴△OCD为等腰直角三角形,∠ODC=45°。
∴∠ECD=∠ODC,∴CE∥x轴。
∴点C、E关于对称轴(直线x=2)对称,
∴点E的坐标为(4,1)。
如答图①所示,设对称轴(直线x=2)与CE交于点F,

则F(2,1)。
∴ME=CM=QM=2。
∴△QME与△QMC均为等腰直角三角形。
∴∠QEC=∠QCE=45°。
又∵△OCD为等腰直角三角形,
∴∠ODC=∠OCD=45°。
∴∠QEC=∠QCE=∠ODC=∠OCD=45°。∴△CEQ∽△CDO。
(4)存在。
如答图②所示,作点C关于直线QE的对称点C′,作点C关于x轴的对称点C″,连接C′C″,交OD于点F,交QE于点P,则△PCF即为符合题意的周长最小的三角形,由轴对称的性质可知,△PCF的周长等于线段C′C″的长度。
(证明如下:不妨在线段OD上取异于点F的任一点F′,在线段QE上取异于点P的任一点P′,连接F′C″,F′P′,P′C′.
由轴对称的性质可知,△P′CF′的周长=F′C″+F′P′+P′C′。
而F′C″+F′P′+P′C′是点C′,C″之间的折线段,
由两点之间线段最短可知:F′C″+F′P′+P′C′>C′C″,即△P′CF′的周长大于△PCE的周长。)
如答图③所示,连接C′E,

∵C,C′关于直线QE对称,△QCE为等腰直角三角形,
∴△QC′E为等腰直角三角形。
∴△CEC′为等腰直角三角形。
∴点C′的坐标为(4,5)。
∵C,C″关于x轴对称,∴点C″的坐标为(﹣1,0)。
过点C′作C′N⊥y轴于点N,则NC′=4,NC″=4+1+1=6,
在Rt△C′NC″中,由勾股定理得:
![]() 。
。
综上所述,在P点和F点移动过程中,△PCF的周长存在最小值,最小值为![]() 。
。
【解析】(1)利用待定系数法求出直线解析式。
(2)利用待定系数法求出抛物线的解析式。
(3)关键是证明△CEQ与△CDO均为等腰直角三角形。
(4)如答图②所示,作点C关于直线QE的对称点C′,作点C关于x轴的对称点C″,连接C′C″,交OD于点F,交QE于点P,则△PCF即为符合题意的周长最小的三角形,由轴对称的性质可知,△PCF的周长等于线段C′C″的长度。
利用轴对称的性质、两点之间线段最短可以证明此时△PCF的周长最小。
如答图③所示,利用勾股定理求出线段C′C″的长度,即△PCF周长的最小值。

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案【题目】某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
销售单价(元) | x |
销售量y(件) |
|
销售玩具获得利润w(元) |
|
(2)在(1)问条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元.
(3)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?